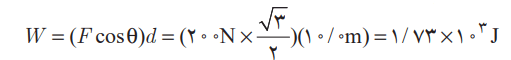رپیتیچ > بلاگ > آموزش درس 2 فصل 3 فیزیک دهم + تدریس ویدیویی

آموزش درس 2 فصل 3 فیزیک دهم + تدریس ویدیویی

آنچه در این پست میخوانید

آموزش درس 2 فصل 3 فیزیک دهم به‌صورت تست‌بیس، همراه با تدریس ویدیویی «شهاب نصیری» را، در این پست از رپیتیچ ببینید.

در جلسه قبل با انرژی جنبشی، فرمول و یکاهای آن آشنا شدیم. درس دوم این فصل به کار انجام شده‌ توسط نیروی ثابت اختصاص دارد.

برای دسترسی به کل مباحث فصل سوم، روی لینک زیر کلیک کنید.

خب، اول از همه بریم که ویدیوی آموزشی این بخش رو ببینیم.

آموزش ویدیویی درس 2 فصل 3 فیزیک دهم

در این قسمت، بخشی از «آموزش درس دوم فصل سوم فیزیک دهم» را به‌صورت ویدیویی می‌توانید ببینید. مدرس این قسمت، جناب مهندس شهاب نصیری، مولف برتر آزمون‌های موسسات معتبر هستند.

فرم دریافت آموزش های ویدئویی فیزیک:

اگه تو هم میخوای کل فیزیکت رو تو کمترین زمان و با تدریس انیمیشنی مفهومی تستی مهندس شهاب نصیری جمع کنی؛ کافیه این فرم رو پر کنی و منتظر تماسمون باشی:

روی نمره 20 و درصد بالای 70 فیزیکت (مثل رتبه های برتر هر سالمون) حساب کن!

لازمه‌ درک درست این درس، آگاهی و دانستن‌ مفاهیم علوم هفتم است. علاوه بر آن، با انرژی جنبشی که در درس قبل یاد گرفتید نیز، رابطه مستقیمی دارد. گاهی اوقات نیروی وارده‌ بر جسم، ممکن است دارای زاویه باشد. این مورد و کار کل را هم در سایت رپیتیچ بررسی خواهیم کرد.

کار انجام شده‌ توسط نیروی ثابت؛ درس دوم فصل سوم فیزیک دهم

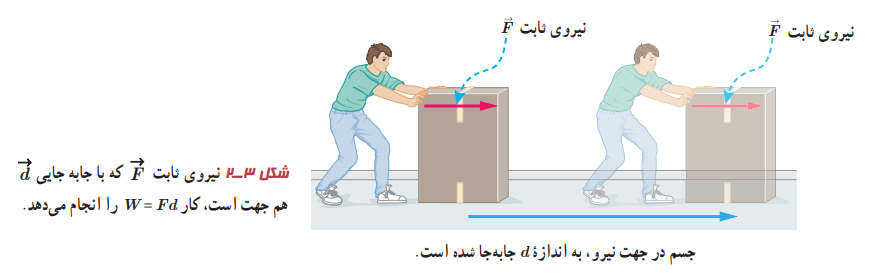
مفهوم کار در فیزیک، با مفهوم آن در زندگی روزمره بسیار متفاوت است. فرض کنید نیروی وارد شده‌ به جسم، ثابت و با جابه‌جایی جسم در یک جهت باشد.

در این صورت کار را می‌توان طبق فرمول زیر محاسبه و به دست آورد:

W = Fd (2-3 رابطه)

در این رابطه F اندازه نیروی وارد بر جسم و d اندازه جابه‌جایی آن است. کار، همان یکای انرژی را دارد و کمیتی نرده‌ای است. برای استفاده از این رابطه به منظور محاسبه کار باید به دو نکته توجه کرد. اول آنکه، نیروی ثابت وارد بر جسم باید با جابه‌جایی آن هم جهت باشد. دوم آنکه، باید بتوان جسم را مانند یک ذره فرض کرد (بخش مدل‌سازی را در فصل اول ببینید).

مثال 3-2

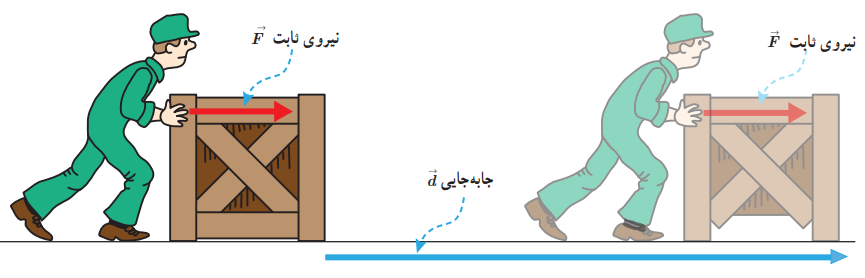
شکل زیر کارگری را در حال هل دادن‌ جعبه‌ای با نیروی ثابت 250N نشان می‌دهد. اگر جعبه 14m در امتداد نیرو جابه‌جا شود، کار انجام شده‌ توسط این نیرو چقدر است؟

پاسخ: اندازه نیروی وارد شده‌ به جعبه، ثابت و با جابه‌جایی جعبه هم جهت است. بنابراین، از رابطه 3-2 داریم:

W = Fd = (250N)(14m) = 3/5 × 10³J

مثال 3-3

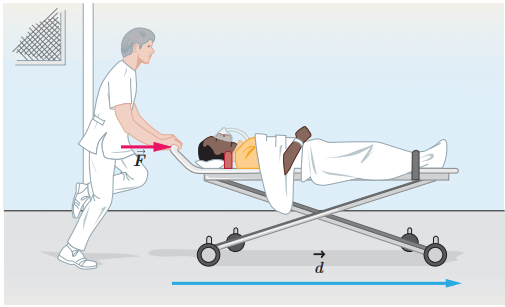
بیماری به جرم 72kg روی تختی به جرم 15kg دراز کشیده‌ است. پرستاری این تخت را با نیروی ثابت و افقی ^→F روی سطحی هموار و با اصطکاک ناچیز هل می‌دهد. مجموعه تخت و بیمار با شتاب 0/60m/s² حرکت می‌کند.

الف) اندازه نیروی ^→F چقدر است؟

ب) اگر تخت 10m در جهت این نیرو جابه‌جا شود، کار انجام‌شده توسط نیروی ^→F را حساب کنید.

پاسخ: الف) جرم کل بیمار و تخت برابر 87kg است. با استفاده از قانون دوم نیوتون داریم:

F = ma = (87kg)(0/60m/s²) = 52N

ب) نیرو و جابه‌جایی در این سوال در یک جهت هستند. با استفاده از رابطه (3-2) کار نیروی F را می‌توان محاسبه کرد:

W = Fd = (52N)(10m) = 5/2 × 10²J

تمرین 3-3

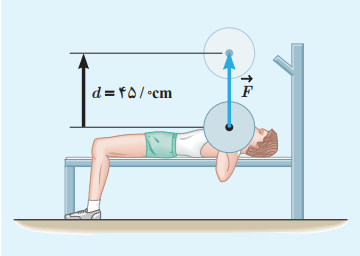
ورزشکاری وزنه‌ای به جرم 65kg را به طور یکنواخت، 45cm بالای سر خود می‌برد.

کاری که این ورزشکار روی وزنه انجام داده‌ است را محاسبه کنید. اندازه شتاب گرانش زمین را g=9/8N/kg بگیرید.

پاسخ: در نظر بگیرید که جسم با تندی یکنواخت به سمت بالا حرکت می‌کند. در این حالت نیرویی که به جسم وارد می‌شود، همان وزن آن است. در تمرین 3-3، نیرو و جهت جابه‌جایی جفت‌شان به سمت بالا هستند. بنابراین زاویه بین نیرو و جابه‌جایی صفر است (Θ=0):

W = F (cosΘ) d = mg (cosΘ) d =

65 × 9/8 × (cos0^°) × 0/45 = 286/65J

مهارت‌های ریاضی (یادآوری از ریاضی سال‌های هشتم و دهم)

در ریاضی سال هشتم با تجزیه یک بردار روی محورهای x و y آشنا شدید. همچنین نوشتن‌ مولفه‌های آن بر حسب بردارهای یکه ^→i و ^→j را یاد گرفتید.

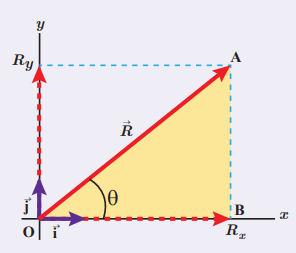
اگر R_x و R_y مولفه‌های بردار ^→R روی محورهای x و y باشند، می‌توان نوشت:

R^→ = R_x i^→ + R_yj^→

در ریاضی سال دهم نیز تا حدودی با مثلث قائم‌الزاویه آشنا شدید. مثلث OAB شکل بالا را در نظر بگیرید. توابع مثلثاتی سینوس و کسینوس آن برای زاویه Θ به صورت زیر محاسبه می‌شود:

اگر اندازه بردار ^→R را با R نشان دهیم، با توجه به شکل بالا داریم:

OA = R و OB = R_x و AB = R_y

به این ترتیب، مولفه‌های بردار ^→R را می‌توان به صورت زیر نوشت:

R_x = RcosΘ و R_y = RsinΘ

با جایگذاری دو رابطه آخر در رابطه اول، می‌توان یک بردار را بر حسب توابع مثلثاتی سینوس و کسینوس نوشت. به این ترتیب داریم:

R^→ = RcosΘ i^→ + RsinΘ j^→

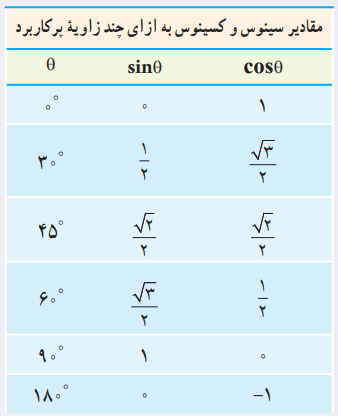
در جدول پایین، مقادیر سینوس و کسینوس به ازای چند زاویه پرکاربرد را می‌بینید.

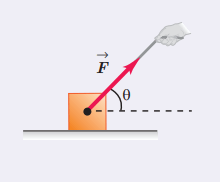
فرض کنید مطابق شکل پایین، جسمی را با نیروی ^→F می‌کشیم.

مولفه افقی این نیرو F_x=FcosΘ و مولفه قائم آن F_y=FsinΘ است. در این دو مولفه، F، اندازه نیروی ^→F است.

محاسبه کار هنگام نیروی ثابت زاویه دار

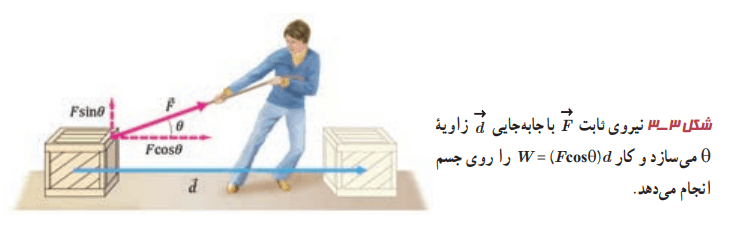
تعریف کار بر اساس رابطه 3-2 تنها برای حل مسئله‌هایی به کار می‌رود که نیرو و جابه‌جایی در یک جهت باشند. در نظر بگیرید مطابق شکل 3-3 نیروی وارد شده‌ به جسم با جابه‌جایی زاویه Θ بسازد.

در این حالت نیروی ^→F دارای دو مولفه است؛ یکی موازی با جابه‌جایی و دیگری عمود بر آن. مولفه‌ای از نیرو که بر جابه‌جایی عمود است (F_y) کاری روی جسم انجام نمی‌دهد. کار انجام شده‌ روی جسم تنها ناشی از مولفه‌ای از نیرو است که در راستای جابه‌جایی است (F_x). کاری که نیروی ثابت ^→F به ازای جابه‌جایی ^→d روی جسم انجام می‌دهد، اینگونه محاسبه می‌شود:

مثال 3-4

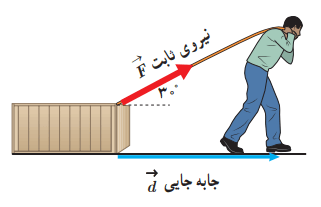
در شکل پایین شخصی جعبه‌ای را با نیروی ثابت 200N روی سطحی هموار و با اصطکاک ناچیز، به اندازه 10m جابه‌جا می‌کند.

الف) کار انجام شده‌ توسط این نیرو چقدر است؟

ب) نیروهای دیگری را که بر جسم وارد می‌شود مشخص کنید. کاری را که هر کدام از این نیروها روی جسم انجام می‌دهند حساب کنید.

پاسخ: الف) با جایگذاری اطلاعات داده‌ شده‌ و کسینوس 30 درجه در رابطه 3-3 داریم:

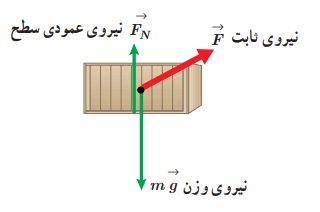
ب) نیروی وزن و نیروی عمودی سطح بر جابه‌جایی عمودند که در شکل پایین مشخص کرده‌ایم.

با این حساب این نیروها کاری روی جسم انجام نمی‌دهند. (توجه کنید که cosΘ=cos90^°=0)

تمرین 3-4

تمرین 3-3 را دوباره ببینید. کار انجام شده‌ توسط ورزشکار را روی وزنه برای حالتی دیگر حساب کنید. در نظر بگیرید ورزشکار با وارد کردن‌ همان نیروی ^→F، وزنه را به آرامی پایین می‌آورد. در دو حالت چه تفاوتی بین مقادیر به دست آمده‌ کار انجام شده‌ وجود دارد؟

پاسخ: در این حالت وزنه بردار نیرویی به سمت بالا را به وزنه وارد کرده‌ و به آرامی پایین می‌آورد. با این حساب نیرو به سمت بالاست، ولی جابه‌جایی به سمت پایین. پس زاویه‌ای که ایجاد می‌شود، 180 درجه خواهد بود:

W = F (cosΘ) d = mg (cosΘ) d =

65 × 9/8 × (cos180^°) × 0/45 = -286/65J

پرسش 3-2

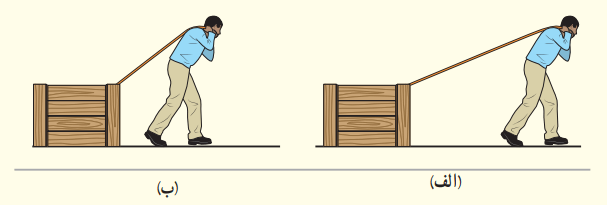
شخصی جسمی را یک بار با طنابی بلند و بار دیگر با طنابی کوتاه‌تر روی سطحی هموار می‌کشد. فرض کنید جابه‌جایی و کاری که این شخص در هر دو بار روی جعبه انجام می‌دهد، یکسان باشد. به نظر شما در کدام حالت، شخص نیروی بزرگ‌تری وارد کرده‌ است؟ اصطکاک را در هر دو حالت، ناچیز به شمار آورید.

پاسخ: می‌دانیم که رابطه کار برابر W=F(cosΘ)d است. از طرف دیگر کار و جابه‌جایی در هر دو حالت یکسان است. با این حساب مقادیر FcosΘ در حالت الف و ب یکسان است، یعنی:

F(cosΘ)_الف = F(cosΘ)_ب

توجه کنید در حالت ب که طناب کوتاه‌تر است، زاویه بیشتری با افق دارد. هر چه زاویه بیشتر باشد، کسینوس آن کمتر می‌شود، پس

F_الف < F_ب ⇐ (cosΘ)_الف > (cosΘ)_ب

کار کل

در نظر بگیرید که به جای یکی، چند نیرو بر جسمی وارد بشود. با استفاده از رابطه 3-3 می‌توان کار انجام شده‌ توسط هر نیرو را به طور جداگانه محاسبه کرد. سپس با جمع جبری کار انجام شده‌ توسط تک‌تک نیروها کار کل (W_t) را به دست می‌آوریم.

مثال 3-5

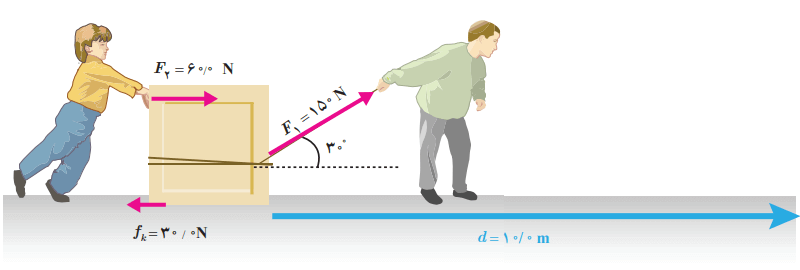
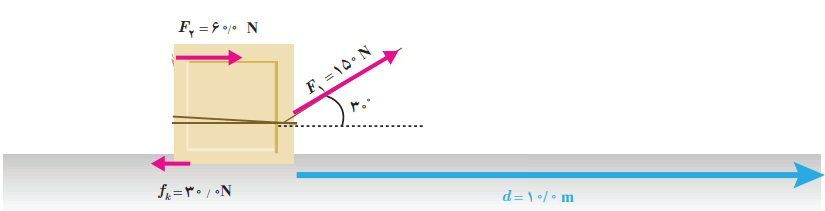
شکل زیر پدر و پسری را در حال جابه‌جا کردن‌ یک جعبه سنگین روی سطحی هموار نشان می‌دهد. نیروی F₁ را پدر و نیروی F₂ را پسر به جسم وارد می‌کنند. در این شکل، f_k نیروی اصطکاک جنبشی است که با حرکت جسم مخالفت می‌کند. این نیرو در خلاف جهت جابه‌جایی، به جعبه وارد می‌شود. کار کل انجام شده‌ روی جسم را محاسبه کنید.

پاسخ: اول از همه، کار انجام شده‌ توسط هر نیرو را به طور جداگانه محاسبه می‌کنیم. برای محاسبه کار نیروی F₁، اطلاعات داده‌ شده‌ و معادل کسینوس 30 درجه را در رابطه 3-3 جایگذاری می‌کنیم. به این ترتیب داریم:

W₁ = (F₁cosΘ) d = (150N × √3/2) (10/0m) = 1/30 × 10³J

چون پسر جعبه را در جهت جابه‌جایی هل می‌دهد، کار انجام شده‌ توسط نیروی F₂ برابر است با:

W₂ = F₂d = (60/0N) (10/0m) = 600J

در محاسبه کار نیروی f_k، باید معادل کسینوس 180 درجه را در نظر بگیریم که برابر منفی یک است. پس:

W₃ = (f_kcosΘ) d = (30/0N × (-1)) (10/0m) = -300J

کار کل انجام شده‌ با جمع جبری مقدار کار انجام شده‌ توسط تک‌تک نیروها برابر است. توجه کنید که کار نیروی وزن و نیروی عمودی تکیه‌گاه صفر است. به این ترتیب داریم:

W_t = W₁ + W₂ + W₃ = 1/30 × 10³J + 600J + (-300J) = 1/60 × 10³J

تمرین 3-5

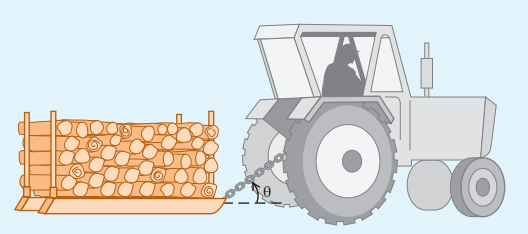
کشاورزی توسط تراکتور، سورتمه‌ای پر از هیزم را در راستای یک زمین هموار به اندازه 200m جابه‌جا می‌کند.

وزن کل سورتمه و بار آن mg=15000N است. تراکتور نیروی ثابت F₁=550N را در زاویه Θ=45^° بالای افق به سورتمه وارد می‌کند. نیروی اصطکاک جنبشی f_k=3500N است که برخلاف جهت حرکت به سورتمه وارد می‌شود. کار کل انجام شده‌ روی سورتمه را محاسبه کنید.

پاسخ: قبل از حل این تمرین، بهتر است که یک بار دیگر، به مثال 3-5 توجه بکنید.

تمرین 3-5 را به دو روش می‌توان حل کرد و به پاسخ رسید.

روش اول: ابتدا کار تمام نیروها را به دست می‌آوریم. سپس همه آنها را با هم جمع می‌کنیم تا کار کل به دست بیاید.

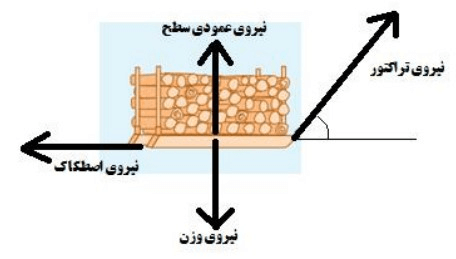
نیروهای وارد بر سورتمه، شامل این موارند:

نیروی تراکتور
نیروی وزن
نیروی عمودی سطح (که از طرف سطح وارد می‌شود)
نیروی اصطکاک (خلاف جهت حرکت)

کار نیروی وزن و کار نیروی عمودی سطح، صفر است. جهت حرکت سورتمه به سمت راست است، ولی جهت این دو نیرو به سمت بالا و پایین است. بنابراین زاویه نیرو و جابه‌جایی 90 درجه است. هرگاه زاویه نیرو و جابه‌جایی 90 درجه باشد، کار آن نیرو صفر می‌شود.

W_وزن = W_عمودی = Zero

W_{تراکتور} = F (cosΘ) d = 5500 × (cos45^°) × 200 = 770000J

W_اصطکاک = F (cosΘ) d = 3500 × (cos180^°) × 200 = -700000J

W_کل=W_{تراکتور}+W_اصطکاک+W_وزن+W_عمودی

770000J + (-700000J) + 0 + 0 = 70000J

روش دوم: مولفه‌های نیرو در امتداد جابه‌جایی را محاسبه می‌کنیم. نیروی خالص وارد بر سورتمه و سپس، کار نیروی خالص را به دست می‌آوریم.

نیروهای وزن و عمودی سطح، مولفه افقی ندارند (به سمت چپ و راست نیرویی وارد نمی‌کنند).

مولفه افقی نیروی تراکتور، اصطکاک و سپس نیروی خالص به صورت زیر به دست می‌آید:

تراکتورF_x = F(cosΘ) = 5500 × cos45^° = 3850N

اصطکاکf_x = F(cosΘ) = 3500 × cos180^° = -3500N

خالصF_T = F_x + f_x = 3850N + (-3500N) = +350N

علامت مثبت نشان می‌دهد نیرو در جهت جابه‌جایی وارد می‌شود. کار کل برابر است با:

W_T = F_Td = 350 × 200 = 70000J