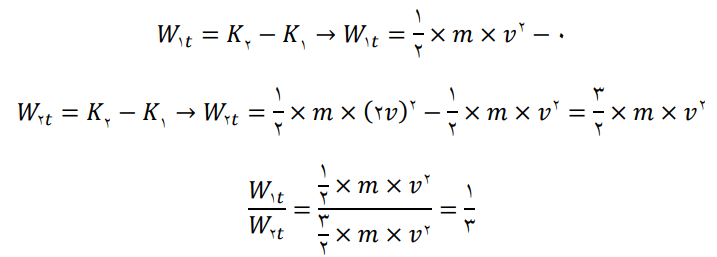رپیتیچ > بلاگ > آموزش درس 3 فصل 3 فیزیک دهم + تدریس ویدیویی

آموزش درس 3 فصل 3 فیزیک دهم + تدریس ویدیویی

آنچه در این پست میخوانید

آموزش درس 3 فصل 3 فیزیک دهم به‌صورت تست‌بیس، همراه با تدریس ویدیویی «شهاب نصیری» را، در این پست از رپیتیچ ببینید.

در جلسه قبل با کار انجام شده‌ توسط نیروی ثابت آشنا شدیم. درس سوم این فصل به کار و انرژی جنبشی اختصاص دارد.

برای دسترسی به کل مباحث فصل سوم، روی لینک زیر کلیک کنید.

خب، اول از همه بریم که ویدیوی آموزشی این بخش رو ببینیم.

آموزش ویدیویی درس 3 فصل 3 فیزیک دهم

در این قسمت، بخشی از «آموزش درس سوم فصل سوم فیزیک دهم» را به‌صورت ویدیویی می‌توانید ببینید. مدرس این قسمت، جناب مهندس شهاب نصیری، مولف برتر آزمون‌های موسسات معتبر هستند.

فرم دریافت آموزش های ویدئویی فیزیک:

اگه تو هم میخوای کل فیزیکت رو تو کمترین زمان و با تدریس انیمیشنی مفهومی تستی مهندس شهاب نصیری جمع کنی؛ کافیه این فرم رو پر کنی و منتظر تماسمون باشی:

روی نمره 20 و درصد بالای 70 فیزیکت (مثل رتبه های برتر هر سالمون) حساب کن!

در درس‌های قبلی با کار و انرژی جنبشی به صورت جداگانه آشنا شده‌اید. جالب است بدانید که این دو مفهوم از هم جدا نیستند و می‌توان ارتباط میان آنها را به دست آورد. در دامه قرار است کار و انرژی جنبشی را یک مفهوم واحد در نظر بگیریم و به بررسی آن بپردازیم.

کار و انرژی جنبشی؛ درس سوم فصل سوم فیزیک دهم

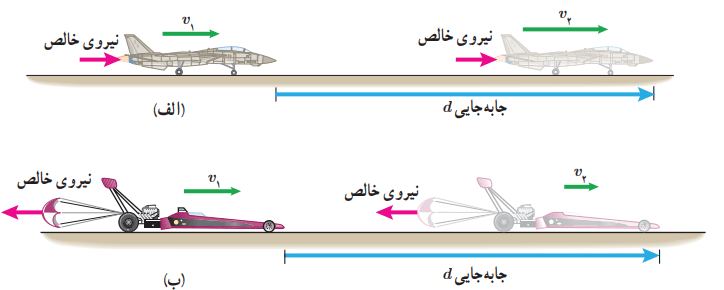
اگر در حین جابه‌جایی جسمی، نیروی خالصی به آن وارد شود، کار کل انجام شده‌ روی جسم ممکن است مثبت یا منفی باشد. در شکل (3-4 الف)، نیروی خالص وارد شده‌ به هواپیما با جابه‌جایی آن هم جهت است. کار کل انجام شده‌ روی هواپیما، سبب افزایش انرژی جنبشی آن شده‌ است.

در شکل (3-4 ب) نیروی خالص برحلاف جهت جابه‌جایی به یک خودروی مسابقه‌ای وارد شده‌ است. کار کل انجام شده‌ روی آن، سبب کاهش انرژی جنبشی اتومبیل شده‌ است.

وقتی نیروی خالصی به جسمی وارد می‌شود، اگر کار مثبتی روی جسم انجام دهد به معنای دادن‌ انرژی به آن است. اگر کار منفی روی جسم انجام دهد، به معنای گرفتن‌ انرژی از آن است.

در شکل (3-4 الف) کار مثبت روی هواپیما انجام شده‌ و انرژی جنبشی آن افزایش یافته‌ است. کار منفی روی خودرو در شکل (ب)، انجام شده‌ و انرژی جنبشی آن کاهش یافته‌ است.

قضیه کار-انرژی جنبشی

بین کار کل انجام شده‌ روی یک جسم و تغییر انرژی جنبشی آن رابطه‌ای وجود دارد. این رابطه به قضیه کار-انرژی جنبشی معروف است. مطابق این قضیه، کار کل انجام شده‌ روی یک جسم با تغییر انرژی جنبشی آن برابر است. فرض کنید که انرژی جنبشی جسمی را در دو وضعیت متفاوت با K₁ و K₂ نشان دهیم. در این صورت کار-انرژی جنبشی با رابطه زیر بیان می‌شود:

هنگامی که 0<W_t است، انرژی جنبشی جسم افزایش می‌یابد (انرژی جنبشی پایانی بزرگ‌تر از انرژی جنبشی آغازی K₁ است). جسم در پایان جابه‌جایی، تندتر از آغاز آن حرکت می‌کند.

هنگامی که W_t=0 است انرژی جنبشی جسم در دو نقطه آغازی و پایانی یکسان (K₂=K₁) و تندی آن نیز در این دو نقطه برابر است.

قضیه کار-انرژی جنبشی تنها برای حرکت یک جسم روی مسیری مستقیم نیست. اگر جسم روی هر مسیر خمیده‌ای هم حرکت کند، می‌توان این قضیه را به کار برد. برای درک بهتر می‌توانید تمرین 3-7 را ببینید. قضیه کار-انرژی جنبشی، قانون جدیدی در فیزیک نیست. این فرمول صرفا کار و انرژی جنبشی را به هم مرتبط می‌سازد و به سادگی می‌توان آن را از قانون دوم نیوتون به دست آورد.

مثال 3-6

توپ فوتبالی به جرم 450g از نقطه پنالتی با تندی 20/0m/s به طرف دروازه شوت می‌شود. توپ با تندی 18/0m/s به دستان دروازه‌بان برخورد می‌کند. کار کل انجام شده‌ روی توپ را که سبب کاهش تندی آن شده‌ است محاسبه کنید.

پاسخ: با استفاده از قضیه کار-انرژی جنبشی به سادگی می‌توان مسئله را حل کرد. ابتدا باید انرژی جنبشی توپ را در دو وضعیت مورد نظر مسئله به دست آورد:

K₁ = ½mv²₁ = ½ (0/450kg)(20/0m/s)² = 90/0J

K₂ = ½mv²₂ = ½ (0/450kg)(18/0m/s)² = 72/9J

به این ترتیب، کار کل انجام شده‌ روی توپ را از رابطه 3-4 محاسبه می‌کنیم:

W_t = K₂ – K₁ = 72/9J – 90/0J = -17/1J

علامت منفی نشان می‌دهد که کار کل انجام شده‌ روی توپ، انرژی جنبشی آن را کاهش داده‌ است.

مثال 3-7

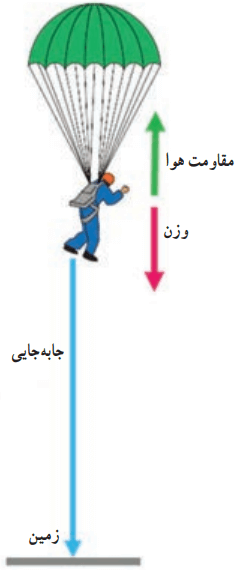
چتربازی به جرم کل 75/0kg، از بالونی که در ارتفاع 800m از سطح زمین است، با تندی 1/20m/s به بیرون بالون می‌پرد. اگر او با تندی 4/80m/s به زمین برسد، کار نیروی مقاومت هوا روی چترباز را در طول مسیر سقوط محاسبه کنید. شتاب گرانش زمین را 9/80m/s² بگیرید.

پاسخ: ابتدا انرژی جنبشی چترباز را در دو وضعیت پریدن‌ از بالون و همچنین رسیدن‌ به سطح زمین به دست می‌آوریم. با توجه به اطلاعات داده‌ شده‌ و همچنین رابطه 3-1 داریم:

K₁ = ½mv²₁ = ½(75/0kg)(1/20m/s)² = 54/0J

K₂ = ½mv²₂ = ½(75/0kg)(4/80m/s)² = 864J

با توجه به شکل در طول حرکت چترباز، دو نیروی وزن و مقاومت هوا به او وارد می‌شود. نیروی وزن در جهت جابه‌جایی و نیروی مقاومت بر خلاف جابه‌جایی است. بنابراین، کار کل برابر مجموع کار این دو نیرو است. به این ترتیب، از رابطه 3-4 داریم:

W_t = K₂ – K₁ = W_وزن+W_{مقاومت هوا}

= 864J – 54/0J = 8/10 × 10²J

با پیدا کردن‌ کار نیروی وزن (mg) و جایگذاری آن در عبارت بالا، کار نیروی مقاومت هوا را به دست می آوریم. از رابطه 3-2 داریم:

W_وزن = mgd = (75/0kg) (9/80m/s²) (800m) = 5/88 × 10⁵J

به این ترتیب، کار نیروی مقاومت هوا برابر است با:

5/88 × 10⁵J + W_{مقاومت هوا}

حاصل این 3 مورد با همدیگر برابر 800J می‌شود. برای به دست آوردن‌ کار نیروی مقاومت هوا تنها باید آن را به یک سمت معادله منتقل کرد. در این صورت مقدار آن برابر 10⁵J×-5/87 می‌شود.

برای اینکه چترباز به طور ایمن و با تندی نسبتا کمی به زمین برسد، کار نیروی مقاومت هوا اثر کاری نیروی وزن را تقریبا خنثی کرده‌ است.

تمرین 3-6

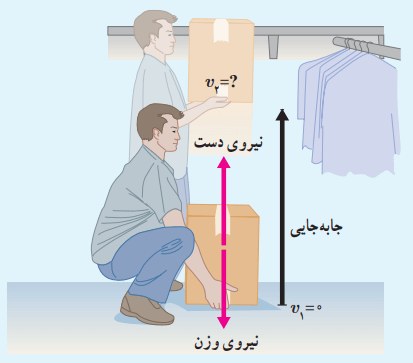
در شکل پایین شخصی با وارد کردن‌ نیروی ثابت 150N، جعبه‌ای به جرم 10kg را از حال سکون در امتداد قائم جابه‌جا می‌کند.

الف) کار انجام شده‌ توسط شخص و کار انجام شده‌ توسط نیروی وزن را روی جعبه تا ارتفاع 1/5m به طور جداگانه حساب کنید.

W_f و W_mg = ?

W_f = F.d.cosΘ = 150 × 1/5 × 1 = 225J

W_mg = mg.d.cos180 = 10 × 10 × 1/5 × (-1) = -150J

ب) کار کل انجام شده‌ روی جعبه تا ارتفاع 1/5m چقدر است؟

W_t = ?

W_t = W_f + W_mg

225 – 150 = 75J

پ) با استفاده از قضیه کار-انرژی جنبشی، تندی نهایی جعبه را در ارتفاع 1/5m حساب کنید.

V₂ = ?

W_t = K₂ – K₁ = ½ m (V²₂ – V²₁)

75 = ½ × 10 (V²₂ – 0) ⇒ 75 = 5V²₂

V²₂ = 75 ÷ 5 = 15

V₂ = √15

تمرین 3-7

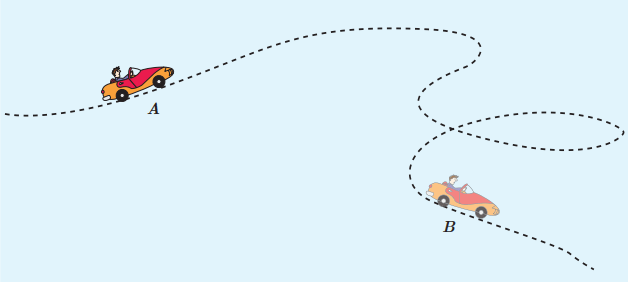
جرم یک خودروی الکتریکی به همراه راننده‌اش 840kg است. وقتی این خودرو از موقعیت A به موقعیت B می‌رود، کار کل انجام شده‌ روی خودرو 73500J است. اگر تندی خودرو در موقعیت A برابر 54/0km/h باشد، تندی آن در موقعیت B چند متر بر ثانیه است؟

پاسخ: با استفاده از قضیه کار و انرژی داریم:

W_کل = K_B – K_A → 73500 = ½ × 840 × V²_B – (½ × 840 × 15²)

73500 = 420 × V²_B – 94500 → 420 × V²_B = 168000 → V²_B = 168000 ÷ 420 = 400

V_B = 20m/s

تمرین 3-8

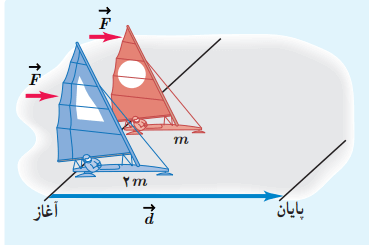
دو قایق بادبانی مخصوص حرکت روی سطوح یخ‌زده با جرم‌های m و 2m را در نظر بگیرید. آنها روی دریاچه افقی و بدون اصطکاکی قرار دارند و نیروی ثابت و یکسان ^→F با وزیدن‌ باد به هر دو وارد می‌شود.

هر دو قایق از حال سکون شروع به حرکت می‌کنند و از خط پایان به فاصله d می‌گذرند. انرژی جنبشی و تندی قایق‌ها را درست پس از عبور از خط پایان، با هم مقایسه کنید.

پاسخ: قضیه کار-انرژی جنبشی را برای هر دو قایق می‌نویسیم:

برای قایق کوچک m₁ را مساوی m در نظر می‌گیریم و از آنجا که K₁ برابر صفر است، داریم:

W_1t = K₂ – K₁ ⇒ W_1t = ½ m v²

در قایق بزرگ m₂ را مساوی 2m در نظر می‌گیریم و از آنجا که ‘K₁ برابر صفر است، داریم:

W_2t = K₂^‘ – K₁^‘ ⇒ W_2t = ½ (2m) v’²

W_1t = W_2t ⇒ V² = 2V^‘2 ⇒ V = √2 V^‘

دیدیم که W_1t = W_2tاست. بنابراین، انرژی جنبشی هر دو قایق، درست پس از عبور از خط پایان با هم برابر است. با این وجود، تندی آنها یکی نیست.

تمرین 3-9

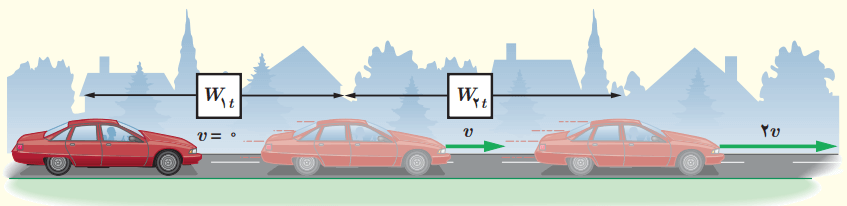
برای آنکه تندی خودرویی از حال سکون به v برسد، باید کار کل W_1t روی آن انجام شود. همچنین برای آنکه تندی خودرو از v به 2v برسد، باید کار کل W_2t روی آن انجام شود. نسبت W_1t/W_2t چقدر است؟

پاسخ: تمرین 3-9 صفحه 64 را به شکل زیر می‌توان جواب داد: