رپیتیچ > بلاگ > آموزش درس 4 فصل 3 فیزیک دهم + تدریس ویدیویی

آموزش درس 4 فصل 3 فیزیک دهم + تدریس ویدیویی

آنچه در این پست میخوانید

آموزش درس 4 فصل 3 فیزیک دهم به‌صورت تست‌بیس، همراه با تدریس ویدیویی «شهاب نصیری» را، در این پست از رپیتیچ ببینید.

در جلسه قبل با کار و انرژی جنبشی آشنا شدیم. درس چهارم این فصل به کار و انرژی پتانسیل اختصاص دارد.

برای دسترسی به کل مباحث فصل سوم، روی لینک زیر کلیک کنید.

فیلم و جزوه فصل سوم فیزیک دهم

خب، اول از همه بریم که ویدیوی آموزشی این بخش رو ببینیم.

آموزش ویدیویی درس 4 فصل 3 فیزیک دهم

در این قسمت، بخشی از «آموزش درس چهارم فصل سوم فیزیک دهم» را به‌صورت ویدیویی می‌توانید ببینید. مدرس این قسمت، جناب مهندس شهاب نصیری، مولف برتر آزمون‌های موسسات معتبر هستند.

فرم دریافت آموزش های ویدئویی فیزیک:

اگه تو هم میخوای کل فیزیکت رو تو کمترین زمان و با تدریس انیمیشنی مفهومی تستی مهندس شهاب نصیری جمع کنی؛ کافیه این فرم رو پر کنی و منتظر تماسمون باشی:

روی نمره 20 و درصد بالای 70 فیزیکت (مثل رتبه های برتر هر سالمون) حساب کن!

سامانه‌های انرژی پتانسیل باید دارای حداقل دو جسم باشند تا رابطه‌ای میان آنها برقرار شود. در این مقاله از رپیتیچ قرار است با انواع انرژی پتانسیل آشنا بشویم.

کار و انرژی پتانسیل؛ درس چهارم فصل سوم فیزیک دهم

انرژی پتانسیل یا ذخیره‌ای در شکل‌های متنوعی مانند گرانشی، کشسانی و الکتریکی وجود دارد. در درس قبل دانستیم که انرژی جنبشی به حرکت یک جسم وابسته‌ است. انرژی پتانسیل برخلاف آن، ویژگی یک سامانه (دستگاه) است تا ویژگی یک جسم منفرد. به عبارت دیگر، انرژی پتانسیل به مکان اجسام یک سامانه نسبت به یکدیگر بستگی دارد. وقتی انرژی پتانسیل یک سامانه کاهش می‌یابد، به شکل‌های دیگری از انرژی تبدیل می‌شود.

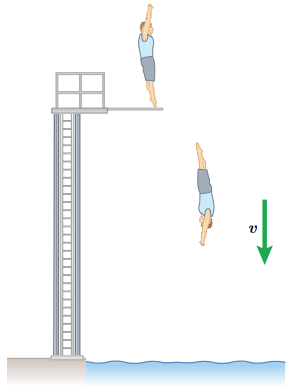
حالتی را تصور کنید که شخصی از یک تخته پرش به درون استخری پر از آب شیرجه می‌زند. در این حال انرژی پتانسیل سامانه شخص-زمین به تدریج به انرژی جنبشی شخص تبدیل می‌شود. در نهایت شخص با تندی نسبتا زیادی با سطح آب برخورد می‌کند.

فنری را توسط جسمی فشرده‌ و سپس رها کنید. انرژی پتانسیل کشسانی سامانه جسم-فنر به انرژی چنبشی جسم تبدیل می‌شود و جسم با تندی زیادی پرتاب می‌شود.

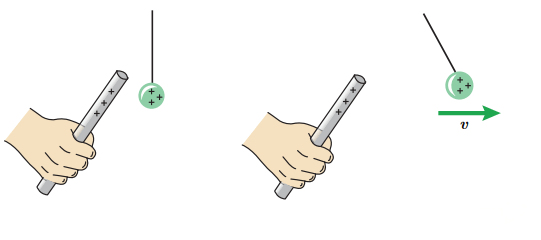
وقتی یک جسم باردار را به جسم باردار دیگر نزدیک‌تر می‌کنیم، بسته‌ به نوع بار، اجسام یکدیگر را می‌ربایند یا می‌رانند. در این حالت انرژی پتانسیل الکتریکی سامانه دو جسم باردار تغییر می‌کند.

انرژی پتانسیل گرانشی

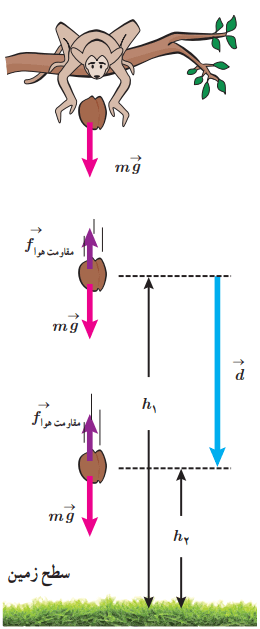
تصویر پایین جسمی به جرم m را نشان می‌دهد که در حال سقوط به طرف زمین است.

در حین سقوط، نیروی وزن ^→mg و نیروی مقاومت هوا _{مقاومت هوا}^→f به آن وارد می‌شود. وقتی جسم از ارتفاع h₁ به ارتفاع h₂ از سطح زمین می‌رسد، کار نیروی وزن در این جابه‌جایی برابر است با:

W_وزن = (mgcosΘ) d = (mgcos0^°) d = mgd

= mg (h₁ – h₂) = – (mgh₂ – mgh₁)

انرژی پتانسیل گرانشی سامانه متشکل از زمین و جسمی به جرم m که در ارتفاع h از سطح زمین است به صورت زیر تعریف می‌شود:

به این ترتیب، کار نیروی وزن را می‌توان به صورت زیر بازنویسی کرد:

رابطه 3-6 نشان می‌دهد کار نیروی وزن برابر با منفیِ تغییر انرژی پتانسیل گرانشی است. همچنین توجه کنید که علامت منها در جلوی ΔU در این رابطه اهمیت زیادی دارد. هنگامی که جسمی رو به پایین حرکت می‌کند، h کاهش می‌یابد. نیروی وزن جسم کار مثبت انجام می‌دهد و انرژی پتانسیل گرانشی کاهش می‌یابد (0>ΔU).

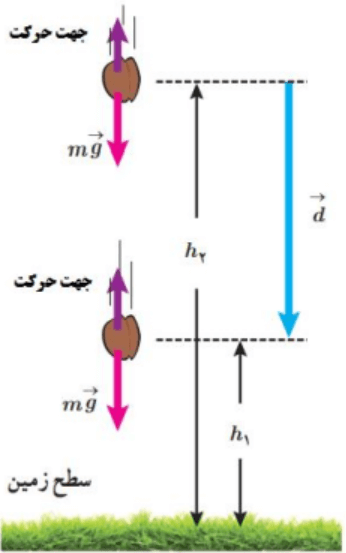
هنگامی که جسمی رو به بالا حرکت می‌کند و از زمین دور می‌شود، h افزایش می‌یابد. در این صورت کار انجام شده‌ توسط نیروی وزن جسم منفی است و انرژی پتانسیل گرانشی آن افزایش می‌یابد (0<ΔU).

ما رابطه 3-6 را برای جسمی که در امتداد قائم و رو به پایین سقوط می‌کرد به دست آوردیم. با این حال می‌توان نشان داد که این رابطه برای هر مسیر دلخواهی برقرار است. به عبارت دیگر، کار نیروی وزن به مسیر بستگی ندارد. این مورد همواره برابر با منفی تغییر انرژی پتانسیل گرانشی سامانه جسم-زمین است.

مثال 3-8

جسمی به جرم 10kg از ارتفاع 2/0m سقوط می‌کند و به زمین می‌رسد. کار نیروی وزن جسم را در این مسیر، (الف) با استفاده از رابطه W=(FcosΘ)d و (ب) با استفاده از رابطه 3-6 محاسبه کنید.

پاسخ:(الف) با استفاده از رابطه W=(FcosΘ)d برای محاسبه کار نیروی وزن داریم،

W=(FcosΘ)d = (mgcosΘ) d

که با توجه به هم جهت بودن‌ نیروی وزن و جابه‌جایی، Θ=0 می‌شود و بنابراین،

W = (10kg) (9/8m/s²) (1) (2/0m) ≈ 2/0 × 10²J

(ب) با استفاده از رابطه 3-6 برای محاسبه کار نیروی وزن داریم،

W_وزن = -ΔU = – (mgh₂ – mgh₁) = -mg (h₂ – h₁)

در صورتی که ارتفاع‌های h₁ و h₂ را نسبت به سطح زمین بسنجیم، h₁=2/0m و h₂=0 می‌شود و بنابراین،

W_وزن = ⇓

– (10kg) (9/8m/s²) (0 – 2/0m) ≈ 2/0 × 10²J

و همان‌طور که می‌بینیم نتیجه دو محاسبه یکسان است.

تمرین 3-10

جسمی به جرم m که رو به بالا حرکت می‌کند و از سطح زمین دور می‌شود را در نظر بگیرید. برای آن نشان دهید که کار نیروی وزن، همچنان از رابطه 3-6 به دست می‌آید. فرض کنید که جسم به اندازه کافی نزدیک به سطح زمین بماند، به گونه‌ای که وزن آن ثابت باشد.

پاسخ: وقتی جسمی به سمت بالا حرکت می‌کند، جهت حرکت رو به بالا و نیروی وزن رو به پایین می‌شود. با این حساب زاویه بین این دو 180 درجه است.

W_وزن = F(cosΘ) = mg(cosΘ) (h₂ – h₁) = -mg (h₂ – h₁) = -ΔU

ویژگی مشترک جسم و زمین

انرژی پتانسیل گرانشی، یک ویژگی مشترک جسم و زمین است و برای سامانه‌ای متشکل از این دو، تعریف می‌شود. بنابراین، U=mgh را باید انرژی پتانسیل گرانشی سامانه جسم-زمین بخوانیم. اگر زمین ثابت بماند و جسم از زمین دور شود، U افزایش می‌یابد و اگر جسم به زمین نزدیک شود U کاهش می‌یابد. توجه کنید که رابطه U=mgh شامل هر دو ویژگی جسم (جرم آن m) و زمین (مقدار g) است.

برخی مواقع و برای سادگی در گفتار، به انرژی پتانسیل گرانشی سامانه جسم-زمین، انرژی پتانسیل گرانشی جسم نیز می‌گویند.

هنگامی که با انرژی پتانسیل گرانشی سروکار داریم، می‌توانیم h=0 را در هر ارتفاعی انتخاب کنیم. اگر مبدا انرژی پتانسیل گرانشی را انتقال دهیم، مقدارهای h₁ و h₂ تغییر می‌کنند و همین طور مقدارهای U₁ و U₂. توجه کنید که این انتقال مبدا، تاثیری بر اختلاف ارتفاع h₂-h₁ یا بر اختلاف انرژی پتانسیل گرانشی U₂-U₁=mg(h₂-h₁) ندارد.

تغییر انرژی پتانسیل گرانشی

کمیتی که در فیزیک اهمیت دارد تغییر انرژی پتانسیل گرانشی (ΔU) بین دو نقطه است، نه مقدار U در یک نقطه خاص. در نتیجه می‌توانیم U را در هر نقطه‌ای که بخواهیم برابر صفر تعریف کنیم، بدون آنکه تاثیری در پاسخ مسئله داشته‌ باشد. این مورد را در مثال بعد، بهتر متوجه می‌شوید.

مثال 3-9

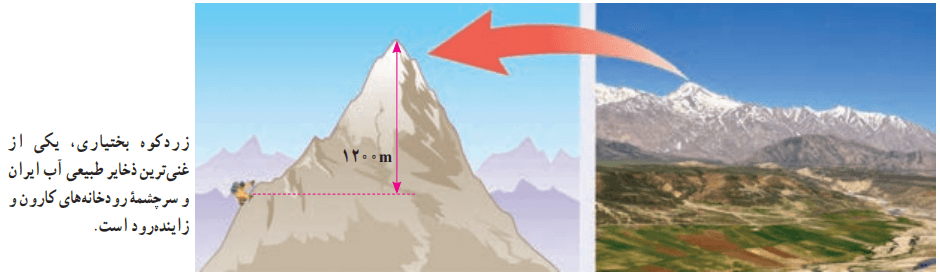
در شکل زیر، کوه‌نوردی به جرم 72/0kg را مشاهده می‌کنید. او در حال صعود به قله زردکوه بختیاری به ارتفاع 4200m از سطح آزاد دریاست. تغییر انرژی پتانسیل گرانشی کوه‌نورد در 1200 متری پایان ارتفاع صعود چقدر است؟ مبدا انرژی پتانسیل گرانشی را (الف) سطح دریا و (ب) قله کوه بگیرید. (g=9/8m/s²)

پاسخ: اگر مطابق فرض (الف)، مبدا انرژی پتانسیل گرانشی را در سطح دریا بگیریم، می‌توان نوشت:

h₁ = 3000m و h₂ = 4200m

ΔU = mg (h₂ – h₁) = (72/0kg) (9/8m/s²) (4200m – 3000m) ≈ 8/5 × 10⁵J

حال اگر مطابق فرض (ب)، مبدا انرژی پتانسیل گرانشی را در قله کوه فرض کنیم، خواهیم داشت:

h₁ = -1200m و h₂ = 0

ΔU = mg (h₂ – h₁) = (72/0kg) (9/8m/s²) [0 -(- 1200m)] ≈ 8/5 × 10⁵J

همان طور که انتظار داشتیم انتقال مبدا انرژی پتانسیل گرانشی، تاثیری در نتیجه نهایی و فیزیک مسئله ندارد.

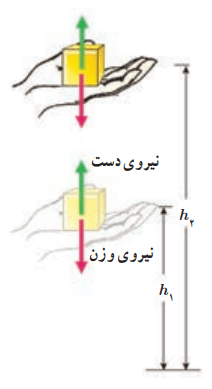
مثال 3-10

جسم ساکنی به جرم m را با دست‌مان از ارتفاع h₁ به ارتفاع h₂ می‌بریم و دوباره به حالت سکون می‌رسانیم. با چشم‌پوشی از مقاومت هوا، کار نیروی دست را در این جابه‌جایی محاسبه کنید.

پاسخ: با استفاده از قضیه کار-انرژی جنبشی (رابطه 3-4) داریم:

W_t = W_وزن + W_دست = K₂ – K₁

از آنجا که جسم در ابتدا و انتهای مسیر ساکن است، تغییر انرژی جنبشی آن صفر است (ΔK=0). از طرف دیگر جمع _وزنW با _دستW برابر صفر می‌شود. با این حساب داریم:

W_دست = -W_وزن

با توجه به رابطه 3-6 می‌توانیم کار نیروی وزن را با استفاده از تغییرات انرژی پتانسیل گرانشی به دست آوریم.

W_وزن = -ΔU = -(mgh₂-mgh₁)

به این ترتیب، کار نیروی دست برابر است با:

W_دست = -(-ΔU) = +(mgh₂-mgh₁)

تمرین 3-11

یک هواپیمای مسافربری به جرم 7/50×10⁴ کبلوگرم با تندی 864km/h در ارتفاع 9/60×10³ متری حرکت می‌کند. انرژی جنبشی و انرژی پتانسیل گرانشی (نسبت به زمین) آن چقدر است؟ مقدار این انرژی‌ها را با هم مقایسه کنید.

پاسخ: اول از همه تندی هواپیما را به متر بر ثانیه تبدیل می‌کنیم:

864km/h = 240m/s

محاسبه انرژی جنبشی:

K = ½ m v² = ½ × 7/5 × 10⁴ × (240)² = 2/16 × 10⁹J

محاسبه انرژی پتانسیل گرانشی:

U = mgh = 7/5 × 10⁴ × 9/8 × 9/60 × 10³ = 7/05 × 10⁹J

پس انرژی پتانسیل گرانشی هواپیما، بیشتر از انرژی جنبشی آن است.

تمرین 3-12

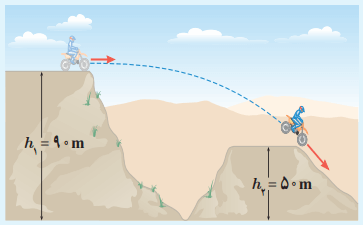
جرم موتور سواری با موتورش 150kg است. این موتورسوار، پرشی مطابق شکل پایین انجام می‌دهد.

الف) انرژی پتاسنیل گرانشی موتورسوار را روی هر یک از تپه‌ها حساب کنید (g=9/8m/s²).

پاسخ:

U₁ = mgh₁ = 150 × 9/8 × 90 = 132300J

U₂ = mgh₂ = 150 × 9/8 × 50 = 73500J

ب) کار نیروی وزن موتورسوار به همراه موتورش را در این جابه‌جایی به دست آورید.

پاسخ: کار نیروی وزن برابر با منفی تغییرات انرژی پتانسیل گرانشی است:

W_وزن = – (U₂ – U₁) = – (73500 – 132300) = 58800J