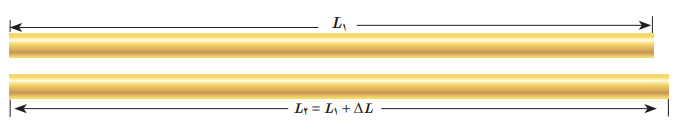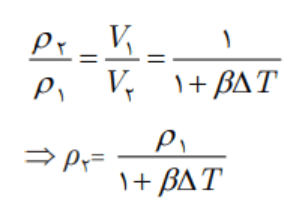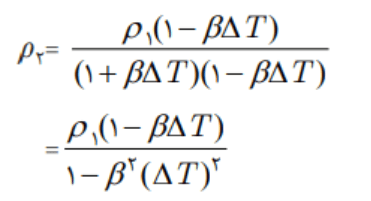آموزش درس 2 فصل 4 فیزیک دهم + تدریس ویدیویی

آموزش درس 2 فصل 4 فیزیک دهم به‌صورت تست‌بیس، همراه با تدریس ویدیویی «شهاب نصیری» را، در این پست از رپیتیچ ببینید.

در جلسه قبل با دما، مقیاس‌های آن و دماسنجی آشنا شدیم. درس دوم این فصل به مفهوم گسترده‌ انبساط گرمایی اختصاص دارد.

برای دسترسی به کل مباحث فصل چهارم، روی لینک زیر کلیک کنید.

فیلم و جزوه فصل چهارم فیزیک دهم

خب، اول از همه بریم که ویدیوی آموزشی این بخش رو ببینیم.

آموزش ویدیویی درس 2 فصل 4 فیزیک دهم

در این قسمت، بخشی از «آموزش درس دوم فصل چهارم فیزیک دهم» را به‌صورت ویدیویی می‌توانید ببینید. مدرس این قسمت، جناب مهندس شهاب نصیری، مولف برتر آزمون‌های موسسات معتبر هستند.

 

 

بر اثر گرما، ممکن است انبساط طولی، سطحی و یا حجمی رخ بدهد. در دل این مباحث، با ضرایب و نحوه محاسبه هر کدام از این موارد نیز آشنا می‌شویم. در نهایت به بررسی این موضوع می‌پردازیم که چرا انبساط آب، غیر عادی است.

انبساط گرمایی؛ درس دوم فصل چهارم فیزیک دهم

اگر درِ یک ظرف شیشه‌ای محکم باشد، معمولا برای باز کردن‌ درِ ظرف، روی آن آب داغ می‌ریزیم. حالتی را در نظر بگیرید که دو لیوان شیشه‌ای درهم، گیر کرده‌ باشند. اگر در لیوان داخلی آب سرد بریزیم و لیوان بیرونی را در آب گرم بگذاریم، می‌توان آنها را از هم جدا کرد. دندانپزشکان برای پر کردن‌ سوراخ دندان، از ماده‌ای که مشخصه‌های انبساط گرمایی دندان را دارد، استفاده می‌کنند.

در غیر این صورت، خوردن‌ و آشامیدن‌ حس ناخوشایند و همراه با دردی خواهد داشت. فرض کنید که یک بستنی می‌خورید و بعد از آن، تصمیم می‌گیرید یک فنجان چای داغ بنوشید. اگر ماده‌ ویژگی‌های انبساط گرمایی متناسب را نداشته‌ باشد، حتی ممکن است دندان بشکند.

بیشتر اجسام با افزایش دما حجم‌شان زیاد و با کاهش دما حجم‌شان کم می‌شود. این پدیده‌ اساس ساخت بعضی از دماسنج‌هاست. بی‌توجهی به پدیده‌ انبساط می‌تواند مشکلاتی را ایجاد سازد. از این موارد می‌شود به ساختن‌ پل‌ها، ساختمان‌ها، خط‌آهن‌ها، خطوط انتقال نیرو و سوخت اشاره کرد.

پرسش 4-1

الف) چرا بهتر است قفل و کلید یک در، هم‌جنس باشند؟

پاسخ: موردی که باید همیشه در نظر داشته‌ باشیم، توجه به تغییرات دمایی (انبساط و انقباض گرمایی) است. اگر قفل و کلید از یک جنس باشند، در صورت تغییر دما، ابعاد هر دو جسم به یک اندازه تغییر می‌کند. با این حساب، کلید درون قفل گیر نمی‌کند.

ب) چرا در برخی از فصل‌های سال، بعضی از درها در چارچوب خود گیر می‌کنند؟

پاسخ: به دلیل انبساط‌های گرمایی متفاوت در و چارچوب آن، تغییرات ابعاد آنها یکسان نخواهد نبود. در نتیجه، ممکن است که درها در چارچوب خود گیر بکنند.

فعالیت 4-3

1- شکل (الف) تصویری واقعی از دو قسمت متوالی خط‌آهن (ریل راه‌آهن)های قدیمی را در گذشته‌ نشان می‌دهد. اگر فاصله خالی بین این دو قسمت به حد کافی زیاد نباشد، چه مشکلی پیش می‌آید؟

پاسخ: با افزایش دما ریل‌ها منبسط شده‌ و به هم نیرو وارد می‌کنند. در نتیجه باعث خمیدگی یکدیگر می‌شوند. با کاهش دما و انقباض ریل‌ها نیز، اتصالات از هم جدا می‌شوند.

2- امروزه بین قسمت‌های متوالی خط آهن فاصله‌ای در نظر گرفته‌ نمی‌شود. این قسمت‌ها پشت سرهم جوشکاری می‌شوند.

در این روش چگونه مشکل ناشی از انبساط در یک روز گرم تابستانی برطرف می‌شود؟

پاسخ: در این روش ریل‌ها را از زیر به یک پایه وصل کرده‌ و از بالا به هم جوش می‌دهند. در این حالت با یک ریل بسیار بزرگ سروکار داریم. این ریل که از دو طرف آزاد است، می‌تواند به راحتی منبسط بشود.

انبساط طولی

میله‌ای فلزی به طول L=L₁ را در نظر بگیرید. حالا دمای میله را به اندازه ΔT افزایش می‌دهیم. تجربه نشان می‌دهد که طول میله به اندازه ΔL=L₂-L₁ افزایش می‌یابد.

هرچه تغییر دمای میله فلزی بیشتر باشد، افزایش طول بیشتر است. هرچه طول اولیه میله بزرگ‌تر باشد، به ازای یک تغییر دمای مشخص افزایش طول بیشتر خواهد بود.

فرض کنید دمای دو میله هم‌اندازه که جنس‌های متفاوتی دارند را به یک اندازه افزایش دهیم. در این صورت میزان افزایش طول آنها متفاوت است. بنابراین، در تغییرات دمایی به نسبت کوچک، ΔL را می‌توان از رابطه زیر به دست آورد:

ΔL = α L₁ ΔT    (2-4)

ضریب انبساط طولی

به α ضریب انبساط طولی میله می‌گویند که به جنس میله بستگی دارد.

در رابطه 4-2، ΔL و L₁ بر حسب متر (m)، ΔT بر حسب کلوین (K) یا درجه سلسیوس (C°) است. از آنجا یکای α، بر کلوین (1/K) یا بر درجه سلسیوس (C°/1) تعیین می‌شود.

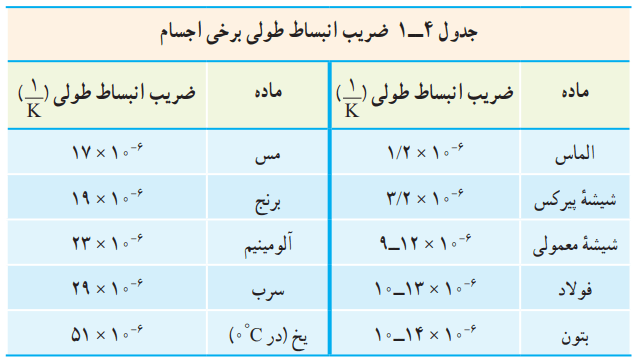
ضریب انبساط طولی برخی اجسام در جدول 4-1 داده‌ شده‌ است.

توجه کنید که مقادیر داده‌ شده‌ برای α در جدول بسیار کوچک است. همچنین ضریب انبساط طولی α علاوه بر جنس ماده، به دما نیز اندکی وابسته‌ است. به دلیل اینکه این وابستگی ناچیز است، معمولا آن را در محاسبات معمولی نادیده می‌گیریم.

مثال 4-1

طول یک پل معلق (شکل الف)، در پایین‌ترین دمای منطقه 1158m است. این پل از نوعی فولاد با α=13×10^-61/°C ساخته‌ شده‌ است. فرض کنید کمترین دمای ممکن 50- درجه سانتی‌گراد و بیشترین دمای ممکن 50+ درجه سانتی‌گراد باشد. بیشترین تغییر طول ممکن پل چقدر است؟

پاسخ: با استفاده از رابطه 4-2 داریم:

ΔL = αL₁ΔT = (13 × 10^-6 1/°C) (1158m) (100 °C) = 1/5m

تغییر طول 1/5m مقدار نسبتا زیادی است. در عمل نمی‌توان فضایی خالی به طول 1/5 متر را برای این تغییر طول روی پل در نظر گرفت. برای رفع این مشکل از تعدادی بست انبساطی انگشتی که از جنس فلز هستند استفاده می‌کنند. شکل (ب)، نوعی از این بست‌ها و شکل (پ)، نمونه‌ای دیگر از این بست‌ها را نشان می‌دهد.

دماسنج نواری دو فلزه

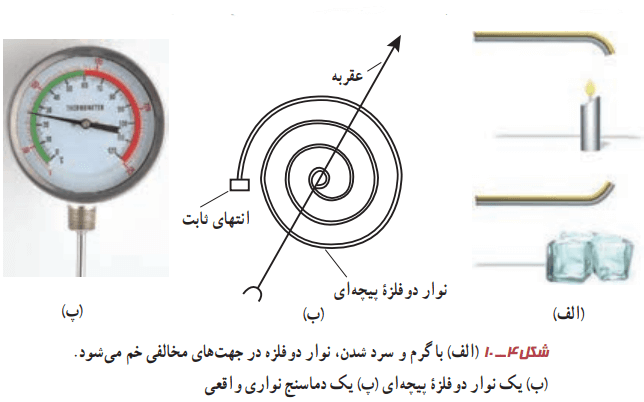
نوار دو فلزه (بی‌متال) از دو تیغه فلزی متفاوت، مانند برنج و آهن ساخته‌ شده‌ است. این دو تیغه سرتاسر به هم جوش داده‌ شده‌ یا پرچ شده‌اند. هرگاه این نوار، گرم یا سرد شود، نوار مانند شکل 4-10 (الف) خم می‌شود. لازم به ذکر است که شکل، با اندکی اغراق رسم شده‌ است. از این ویژگی می‌توان برای دماسنجی و ساختن‌ دماسنج استفاده کرد. به این نوع دماسنج‌ها، دماسنج نواری دو فلزه گفته‌ می‌شود. در شکل 4-10 (ب)، طرحی از این دماسنج را می‌بینید. در آن، از یک نوار دو فلزه پیچه‌ای استفاده شده‌ است. شکل 4-10 (پ) نیز، تصویری واقعی از این نوع دماسنج را نشان می‌دهد.

دماپا (ترموستات)

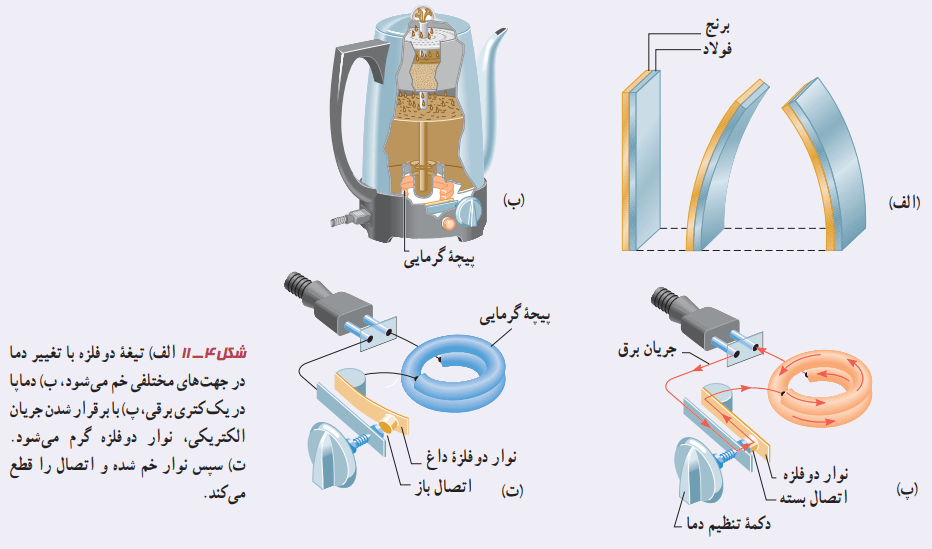
در دماسنج نواری دو فلزه دیدیم که یک نوار دو فلزه با افزایش یا کاهش دما خم می‌شود. نوع این خم‌شدگی در هنگام گرم‌شدن جالب است. تیغه با ضریب انبساط بیشتر، کمان خارجی و تیغه دیگر کمان داخلی را تشکیل می‌دهد (شکل 4-11 الف). از این ویژگی برای ساخت نوعی دماپا (ترموستات) استفاده می‌شود. دماپاها در بسیاری از وسایل الکتریکی مانند یخچال، آبگرم‌کن، کتری برقی و … کاربرد دارند (شکل 4-11 ب). در واقع دماپا کلیدی الکتریکی است که در آن، قطع و وصل جریان با استفاده از حسگرهای گرمایی انجام می‌شود. اغلب از نوارهای دو فلزه به عنوان حسگرهای گرمایی در دماپا استفاده می‌شود. مدار ساده شکل 4-11 پ را ببینید. در این مدار عبور جریان الکتریکی از کتری برقی، باعث گرم‌شدن نوار دو فلزه می‌شود. وقتی دمای نوار به اندازه معینی برسد، بر اثر خم‌شدن نوار، جریان قطع شده‌ و کتری برقی خاموش می‌شود (شکل 4-11 ت).

با خاموش‌شدن کتری، دمای تیغه کاهش می‌یابد و نوار دوباره به شکل وضعیت قبلی خود بازمی‌گردد. به این ترتیب، دوباره مدار وصل شده‌ و کتری برقی روشن می‌شود.

توجیه انبساط گرمایی

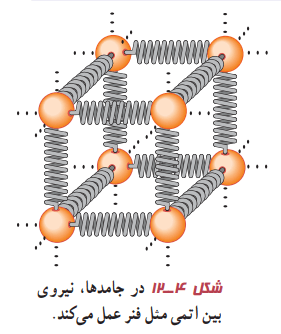
توجیه انبساط گرمایی، مبتنی بر دیدگاه میکروسکوپی است. انبساط گرمایی یک جسم پیامد تغییر فاصله بین اتم‌ها یا مولکول‌های تشکیل‌دهنده آن است. برای درک این مدل، چگونگی رفتار اتم‌ها در یک ماده جامد را درنطر بگیرید. می‌توان اتم‌ها را ذراتی درنظر گرفت که با فنرهایی به اتم‌های مجاور متصل شده‌اند (شکل 4-12).

اتم‌ها پیرامون مکان‌های تعادل خود با دامنه کم، نوسان می‌کنند. می‌توان نشان داد با افزایش دمای جامد، فاصله متوسط بین اتم‌ها افزایش می‌یابد. در نتیجه، جسم جامد منبسط می‌شود.

در مایع با افزایش دما حرکت کاتوره‌ای اتم‌ها و مولکول‌ها بیشتر می‌شود. این افزایش حرکت‌ها باعث دور‌شدن اتم‌ها و مولکول‌ها از هم می‌شود و حجم مایع افزایش می‌یابد.

انبساط سطحی و حجمی

سطح و حجم بیشتر اجسام با افزایش دما زیاد می‌شود. تجربه نشان می‌دهد با انبساط جسم جامد، شکل آن عوض نمی‌شود و همه ابعاد آن به تناسب افزایش می‌یابد.

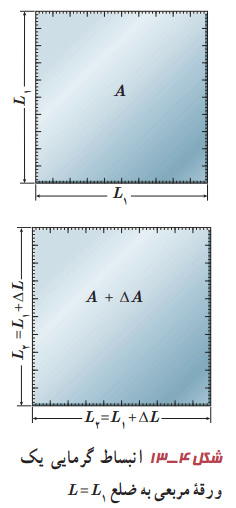
در اینجا ابتدا به انبساط سطحی می‌پردازیم. اگر مساحت اولیه جسم جامد A₁ و افزایش دما ΔT باشد، افزایش مساحتی به اندازه ΔA پیدا می‌کند. در شکل 4-13 این مورد را می‌توانید بهتر متوجه بشوید.

نشان داده‌ می‌شود که این افزایش مساحت به‌طور تقریبی از رابطه زیر به دست می‌آید:

در این رابطه، α ضریب انبساط طولی جسم جامد با یکای بر کلوین یا بر درجه سلسیوس است. یکای ΔA و A₁، متر مربع (m²) و یکای ΔT، کلوین (K) یا درجه سلسیوس (C°) است.

فعالیت 4-4

ورقه‌ای فلزی و مستطیلی‌شکل به اضلاع a₁ و b₁ را درنظر بگیرید. بر اثر افزایش دمای ΔT، طول اضلاع مستطیل به اندازه Δa و Δb افزایش می‌یابند. تصور کنید ضریب انبساط طولی ورقه، α باشد. نشان دهید که افزایش مساحت این ورقه با تقریب مناسب از رابطه ΔA=2αA₁ΔT به دست می‌آید.

پاسخ: با استفاده از معادله 4-2 می‌توان Δa و Δb را به دست آورد:

Δa = α a₁ ΔT ⇒ a₂ = a₁ + α a₁ ΔT ⇒ a₂ = a₁ (1 + α ΔT)

Δb = α b₁ ΔT ⇒ b₂ = b₁ + α b₁ ΔT ⇒ b₂ = b₁ (1 + α ΔT)

مساحت ورقه پس از افزایش دما برابر a₂b₂ است و بنابراین داریم:

A₂ = a₂b₂ = a₁ (1 + α ΔT) a₁ (1 + α ΔT) =

a₁b₁ (1 + α ΔT)

= a₁b₁ (1 + 2 α ΔT + (α ΔT)²)

معمولا α از مرتبه ^5-10 بر درجه سلسیوس است. ΔT هم معمولا بیشتر از مرتبه 10² درجه سلسیوس نیست. می‌شود گفت که جمله ²(αΔT) در مقایسه با جمله 2αΔT بسیار کوچک است و می‌توان از آن چشم‌پوشی کرد. از طرفی a₁b₁ همان مساحت اولیه ورقه است که آن را با A₁ نشان می‌دهیم. بنابراین می‌توان نوشت:

A₂ = A₁ (1 + 2αΔT) ⇒ A₂ – A₁ = ΔA = 2 α A₁ ΔT

مثال 4-2

مساحت یک ورقه مسی 2500cm² است. اگر دمای این ورقه را 50 درجه سانتی‌گراد افزایش دهیم، مساحت آن چقدر افزایش خواهد یافت؟

پاسخ: از رابطه 4-3 استفاده می‌کنیم. ضریب انبساط طولی مس با استفاده از جدول 4-1 برابر ^6-10×17 بر درجه سانتی‌گراد است. بنابراین داریم:

ΔA = 2 α A₁ ΔT = 2 (1/7 × 10^-5/°C) (2500cm²) (50°C) = 4/3cm²

تمرین 4-3

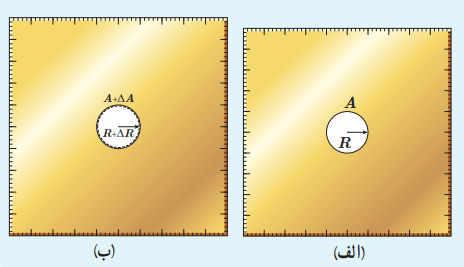
شکل‌های پایین یک ورقه فلزی را قبل و بعد از گرم‌شدن نشان می‌دهد که در مرکز خود حفره‌ای دایره‌ای دارد. اگر ورقه را گرم کنیم، قطر (یا مساحت) حفره بزرگ می‌شود. فرض کنید جنس ورقه، برنجی است و حفره‌ای به قطر یک اینچ (2/54cm) درون آن ایجاد شده‌ است. وقتی دمای ورقه، 200 درجه سانتی‌گراد افزایش یابد، افزایش مساحت حفره چقدر خواهد شد؟

پاسخ: باید از رابطه ΔA=2αAΔT استفاده کنیم. این را می‌توان به طور شهودی دریافت. رابطه ΔA را برای سطح دایره‌ای می‌توان به طور مستقیم نیز اثبات کرد:

ΔA = Δ (πR²) = 2πRΔR = 2πR (αRΔT)

= 2α (πR²) ΔT = 2αAΔT

در هر حال با جایگذاری خواهیم داشت:

ΔT = 2 (19 × 10^-6/°C) (π) ((2/54 × 10^-2m)²/4) (200°C)

= 3/8 × 10^-6 m²

انبساط حجمی

اکنون به انبساط حجمی می‌پردازیم. می‌دانیم که حجم بیشتر اجسام با افزایش دما زیاد می‌شود. فرض کنید حجم اولیه جسم (جامد یا مایع) V₁ و افزایش دما ΔT باشد. در این صورت، جسم افزایش حجمی به اندازه ΔV پیدا می‌کند که از رابطه زیر به دست می‌آید:

در این رابطه، β ضریب انبساط حجمی جامد یا مایع است. یکای ΔV و V₁ متر مکعب (m³) و یکای ΔT، کلوین (K) یا درجه سلسیوس (C°) است. از آنجا، یکای β، بر کلوین یا بر درجه سلسیوس است.

انبساط طولی بیشتر جامدها در راستاهای مختلف، با ضریب انبساط طولی یکسان صورت می‌گیرد. می‌توان نشان داد که ضریب انبساط حجمی این جامدها با تقریب مناسبی سه برابر ضریب انبساط طولی آنهاست.

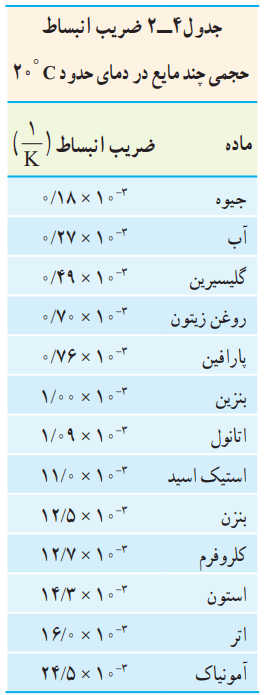
چون مایع‌ها شکل معینی ندارند، انبساط آنها را فقط به صورت حجمی بررسی می‌کنیم. در جدول 4-2 ضریب انبساط حجمی برخی مایعات را مشاهده می‌کنید.

نکته مهم در استفاده از رابطه 4-4 این است که باید بکای ΔV و V₁ یکسان باشد. بیایید ضریب انبساط حجمی جامدها با ضریب انبساط حجمی مایعات را مقایسه کنیم. می‌بینیم که انبساط حجمی جامدها عموما از مایعات کمتر است. به همین دلیل، در بسیاری از محاسبات می‌توان از مقدار افزایش حجم جامد در مقابل افزایش حجم مایع صرف‌نظر کرد.

مثال 4-3

در یک روز داغ تابستان، دمای هوا 40 درجه سانتی‌گراد است. شخصی باک (مخزن) 55 لیتری اتومبیل خود را از بنزین کاملا پر می‌کند. فرض کنید بنزین از منبعی در زیرزمین با دمای 12 درجه سانتی‌گراد بالا آمده‌ باشد. شخص اتومبیل را پارک می‌کند و ساعتی بعد بازمی‌گردد. مشاهده می‌کند بنزین قابل توجهی از باک سرریز شده‌ است. چقدر بنزین از باک بیرون ریخته‌ است؟ (از افزایش حجم باک که بسیار ناچیز است، صرف‌نظر می‌شود.)

پاسخ: از صورت سوال متوجه می‌شویم که بنزین، زمان کافی برای هم‌دما شدن‌ با محیط را در اختیار داشته‌ است. با این حساب، دمای نهایی آن را 40 درجه سانتی‌گراد در نظر می‌گیریم. با استفاده از رابطه 4-4 و جدول 4-2 برای ضریب انبساط حجمی بنزین خواهیم داشت:

ΔV = βV₁ΔT = (1/00 × 10^-3/°C) (55L) (40°C – 12°C) = 1/5L

بنابراین، در کمال تعجب درمی‌یابیم که 1/5 لیتر بنزین روی زمین ریخته‌ است.

مثال 4-4

ارلنی شیشه‌ای با ضریب انبساط طولی ^6-10×9/0 بر سانتی‌گراد در دمای 20 درجه، گنجایشی برابر با 200cm³ دارد. این ارلن را مطابق شکل زیر، با گلیسیرین در همان دما پر کرده‌ایم.

اگر دمای ظرف و گلیسیرین را به 60 درجه سانتی‌گراد برسانیم

الف) آیا گلیسیرین از ظرف بیرون می‌ریزد؟

پاسخ: افزایش حجم گلیسیرین و افزایش گنجایش ظرف را با استفاده از رابطه‌های 4-4 و 4-5 محاسبه می‌کنیم.

ΔV_{گلیسیرین} = β_{گلیسیرین} V₁ ΔT = (49 × 10^-5/°C) (200cm³) (60°C – 20°C) = 3/9cm³

ΔV_ظرف = β_شیشه V₁ ΔT = (3α_شیشه) V₁ ΔT = (3 × 9/0 × 10^-6/°C) (200cm³) (60°C – 20°C) = 0/20cm³

در این محاسبه از جدول 4-2 برای ضریب انبساط حجمی گلیسیرین استفاده کرده‌ایم. از آنجا که افزایش حجم گلیسیرین بیش از افزایش گنجایش ظرف است، پس گلیسیرین از ظرف سرریز می‌شود.

ب) اگر پاسخ قسمت (الف) مثبت است، حجم گلیسیرین سرریز شده‌ چقدر است؟

پاسخ: حجم گلیسیرین سرریز شده‌ برابر است با:

ΔV_{گلیسیرین} – ΔV_ظرف = (3/9cm³-0/20cm³) = 3/7cm³

فعالیت 4-5

آزمایشی را طراحی و اجرا کنید که با آن بتوانید حجم گلیسیرین سرریز شده‌ در مثال 4-4 را اندازه بگیرید. سپس از روی آن، ضریب انبساط حجمی گلیسیرین را تعیین کنید.

پاسخ: این فعالیت در واقع در امتداد مثال 4-4 است. یک ارلن شیشه‌ای را (همراه با یک لوله شیشه‌ای بلند) پر از گلیسیرین می‌کنیم. این کار را باید طوری انجام دهیم که هیچ هوایی در ارلن نباشد و گلیسیرین تا لبه لوله بالا بیاید. سپس ظرف شیشه‌ای بزرگی را پر از آب کرده‌ و آن را داغ می‌کنیم. بعد ارلن را وارد ظرف داغ می‌کنیم. گلیسیرین از لوله جاری می‌شود. حجم گلیسیرین جاری شده‌ را با پیمانه‌ای مدرج اندازه می‌گیریم. باید حجم اولیه گلیسیرین را نیز با با روش مناسبی اندازه‌گیری کرده‌ باشیم. دقت کنید که این حجم، متفاوت از حجم نوشته‌ شده‌ روی ارلن است.

علاوه بر اینها لازم است که دمای اولیه و نهایی گلیسیرین را نیز داشته‌ باشیم. آنگاه همانطور که در مثال 4-4 دیدیم، حجم سرریز شده‌ از رابطه زیر به دست می‌آید:

ΔV_{گلیسیرین}-ΔV_ظرف = (β_{گلیسیرین}-β_ظرف)V₁ΔΘ

با معلوم بودن‌ ضریب انبساط حجمی ظرف، ضریب انبساط حجمی گلیسیرین پیدا می‌شود.

تمرین 4-4

افزایش دما که به طور معمول موجب افزایش حجم اجسام می‌شود، بر جرم آنها تاثیری ندارد. به همین دلیل انتظار داریم که چگالی اجسام با افزایش دما کاهش یابد. رابطه چگالی با تغییر دما به صورت (1+βΔT)/ρ₂=ρ₁ است. در آن ρ₁ و ρ₂ به ترتیب چگالی ماده در دماهای T₁ و T₂، β ضریب انبساط حجمی و T₂-T₁=ΔT است.

الف) رابطه چگالی با تغییر دما را به دست آورید.

پاسخ: این سوال را به دو شکل می‌توان پاسخ داد.

با استفاده از رابطه 4-4 داریم:

ΔV = βV₁ΔT

که آن را می‌توان به صورت زیر نوشت:

V₂ = V₁ (1 + βΔT)

بدیهی است با توجه به اینکه جرم تغییر نمی‌کند، با افزایش دما چگالی جسم باید کاهش یابد. با این حال به چه صورت این قضیه امکان‌پذیر است؟ از رابطه ρ=V/m (تعریف چگالی) داریم:

ب) نشان دهید با تقریب مناسبی می‌توان چگالی جسم را از رابطه ρ₂=ρ₁(1-βΔT) نیز به دست آورد.

پاسخ:صورت و مخرج رابطه بالا را در عبارت پاین ضرب می‌کنیم:

(1-βΔT)

که به این صورت می‌شود:

می‌دانیم که β مقداری کوچک از مرتبه ^3-10 است (جدول 4-2 را ببینید). می‌توانیم از جمله β²(ΔT)² چشم‌پوشی کنیم. با این حساب داریم:

ρ₂ = ρ₁ (1-βΔT)

پاسخ الف و ب به روش دوم:

مثال 4-5

یک قطعه سرب را در دمای اتاق در نظر بگیرید. اگر دمای این قطعه را 200 درجه سانتی‌گراد افزایش دهیم، چگالی آن چند برابر می‌شود؟

پاسخ:

ρ₂ = ρ₁ (1-βΔT) ⇒ ρ₂ ÷ ρ₁ = (1-3αΔT) = 1 – (3 × 29 × 10^-6/°C) (200°C) = 0/98

انبساط غیر عادی آب

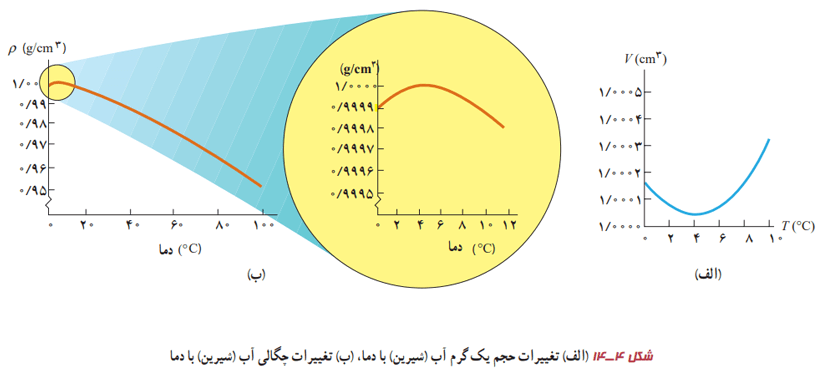
در زمستان‌های سرد، سطح آب آبگیرها و دریاچه‌های کوچک یخ می‌زند و به تدریج یخ ضخیم‌تر می‌شود. با این حال در ته آبگیرها، دمای آب بالاتر از 0 درجه سانتی‌گراد است. این دما برای موجودات زنده‌ای که آنجا زندگی می‌کنند، نسبتا گرم و مناسب است. احتمالا می‌دانید که حجم بیشتر مایع‌ها با کم‌شدن دما کاهش و در نتیجه چگالی آنها افزایش می‌یابد. آب کمی با مایعات دیگر فرق می‌کند. رفتار آب در محدوده دمایی 0 تا 4 درجه سانتی‌گراد متفاوت است. در این محدوده با کاهش دما، حجم آب افزایش و در نتیجه چگالی آن کاهش می‌یابد. شکل‌های 4-14 (الف) و (ب) را ببینید. این اشکال به ترتیب نمودار حجم بر حسب دما و نمودار چگالی برحسب دما را برای آب شیرین نشان می‌دهد. در آنها رفتار غیر عادی آب در محدوده 0 تا 4 درجه سانتی‌گراد دیده‌ می‌شود.

در بازه دمایی 0 تا 4 درجه سانتی‌گراد با افزایش دما، حجم آب کاهش و چگالی آن افزایش می‌یابد. پس از دمای 4 درجه سانتی‌گراد مانند دیگر اجسام، با افزایش دما، حجم افزایش و چگالی کاهش می‌یابد.

چرا آب دریاچه‌ها از بالا یخ می‌زند؟

نغییر حجم غیر عادی آب موجب می‌شود دریاچه‌ها به جای اینکه از پایین به بالا یخ بزنند، از بالا یخ بزنند. فرض کنید دمای سطح آب از 10 درجه سانتی‌گراد اندکی کمتر شود. چگالی آب نسبت به آب زیر خود افزایش می‌یابد و این آب، پایین می‌رود. این رفتار تا رسیدن‌ به دمای 4 درجه سانتی‌گراد ادامه می‌یابد.

می‌دانیم که در دمای پایین‌تر از 4 درجه سانتی‌گراد، حجم آب افزایش و در نتیجه، چگالی آن کاهش می‌یابد. سرد‌شدن بیشتر آب موجب می‌شود که چگالی آب سطح دریاچه نسبت به آب زیر آن کمتر شود. در نتیجه در سطح باقی می‌ماند تا اینکه یخ بزند. در این حالت آب زیر دریاچه هنوز مایع است و دمایی بیش از صفر درجه دارد، ولی سطح آب یخ می‌زند.

حالتی را تصور کنید که آب دریاچه‌ها از پایین به بالا یخ بزند. اثرات زیست‌محیطی زیانبار این پدیده، حیات گیاهی و جانوری را در عمق دریاچه‌ها از بین می‌برد.

 

برای دسترسی به دیگر درس‌های فصل 4 فیزیک 10، روی لینک های زیر کلیک کنید:

• فیلم و جزوه درس یک فصل چهار فیزیک ده
• فیلم و جزوه درس سه فصل چهار فیزیک ده
• فیلم و جزوه درس چهار فصل چهار فیزیک ده
• فیلم و جزوه درس پنج فصل چهار فیزیک ده