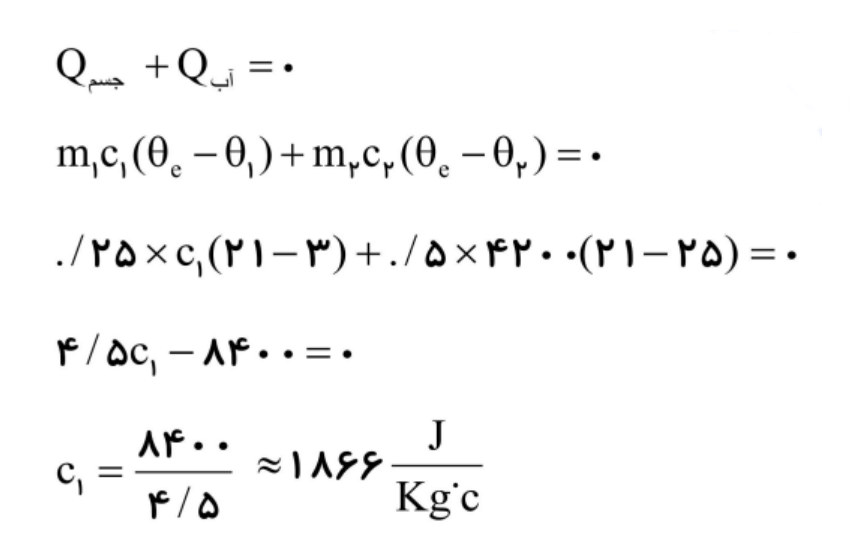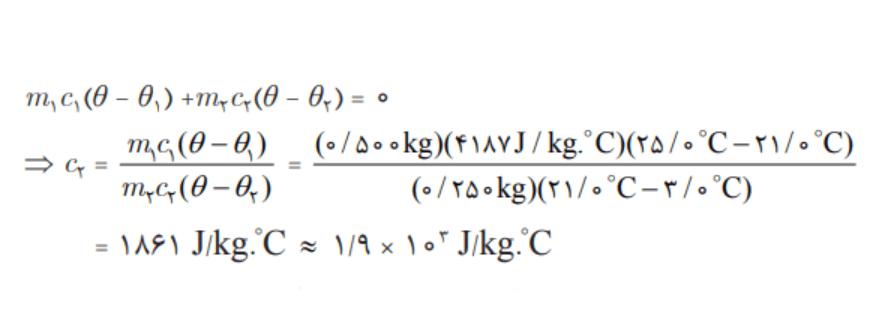رپیتیچ > بلاگ > آموزش درس 3 فصل 4 فیزیک دهم + تدریس ویدیویی

آموزش درس 3 فصل 4 فیزیک دهم + تدریس ویدیویی

آنچه در این پست میخوانید

آموزش درس 3 فصل 4 فیزیک دهم به‌صورت تست‌بیس، همراه با تدریس ویدیویی «شهاب نصیری» را، در این پست از رپیتیچ ببینید.

در جلسه قبل با انبساط گرمایی و به خصوص رفتار غیر عادی آب آشنا شدیم. درس سوم این فصل به صورت تخصصی به مبحث گرما اختصاص دارد.

برای دسترسی به کل مباحث فصل چهارم، روی لینک زیر کلیک کنید.

فیلم و جزوه فصل چهارم فیزیک دهم

خب، اول از همه بریم که ویدیوی آموزشی این بخش رو ببینیم.

آموزش ویدیویی درس 3 فصل 4 فیزیک دهم

در این قسمت، بخشی از «آموزش درس سوم فصل چهارم فیزیک دهم» را به‌صورت ویدیویی می‌توانید ببینید. مدرس این قسمت، جناب مهندس شهاب نصیری، مولف برتر آزمون‌های موسسات معتبر هستند.

فرم دریافت آموزش های ویدئویی فیزیک:

اگه تو هم میخوای کل فیزیکت رو تو کمترین زمان و با تدریس انیمیشنی مفهومی تستی مهندس شهاب نصیری جمع کنی؛ کافیه این فرم رو پر کنی و منتظر تماسمون باشی:

روی نمره 20 و درصد بالای 70 فیزیکت (مثل رتبه های برتر هر سالمون) حساب کن!

گرما مبحثی است که می‌توان با توجه به آن، کارهای متعددی را پیش برد. در ابتدا با تعادل و ظرفیت گرمایی در کنار گرمای ویژه آشنا می‌شویم. دمای تعادل مطلب بعدی است که به آن می‌پردازیم. گرماسنجی نیز موضوع آخر است که با به‌کارگیری آن می‌توان گرماسنج بمبی را درست کرد.

گرما؛ درس سوم فصل چهارم فیزیک دهم

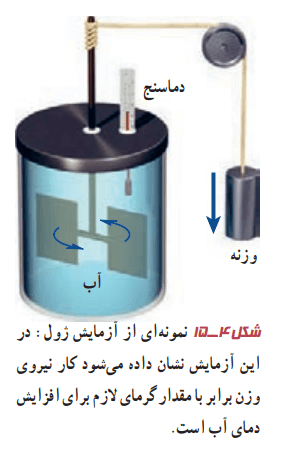
ابتدا درون یک لیوان، آب خیلی سرد بریزید و سپس، لیوان را روی میز اتاق بگذارید. آب گرم می‌شود تا اینکه به دمای هوای اتاق برسد. حالا همین کار را با آب داغ انجام بدهید. آب خنک می‌شود تا اینکه به دمای هوای اتاق برسد. این کرم‌تر یا سردتر شدن‌ در ابتدا به‌سرعت رخ می‌دهد. سپس با آهنگ کندتری ادامه می‌یابد تا اینکه دمای آب با دمای اتاق یکسان گردد. در نهایت به حالتی می‌رسیم که آب، لیوان و هوای اتاق در دمای یکسانی هستند. به این حالت در اصطلاح، تعادل گرمایی می‌گوییم. تا پیش از قرن نوزدهم، چنین مشاهداتی را با پذیرفتن‌ موجودی به نام کالریک توجیه می‌کردند. به عبارتی فرض می‌کردند که چیزی به نام کالریک از جسم گرم به جسم سرد جریان می‌یابد. کنت رامفورد و جیمز پرسکات ژول آزمایش‌هایی را مشابه شکل 4-15 انجام دادند که نتایج جالبی داشت.

آنها دریافتند آنچه که در چنین فرآیندهایی رخ می‌دهد، چیزی جز انتقال انرژی نیست. در مثال آب داغ، انتقال انرژی از آب به محیط پیرامون، سبب کاهش دمای آب می‌شود. در حالت کلی بر اثر اختلاف دمای دو جسم در تماس گرمایی، انرژی از جسم گرم‌تر به جسم سردتر منتقل می‌شود. به این انرژی انتقال یافته‌ بر اثر اختلاف دمای دو جسم، گرما می‌گویند.

توجه کنید اشاره کردن‌ به گرمای موجود در یک جسم اشتباه است. گرما مربوط به انرژی در حال گذار است؛ بنابراین، عبارت‌هایی مانند گرمای یک جسم، نادرست است. گرما را با نماد Q نشان می‌دهند. چون گرما، انرژی انتقال یافته‌ است، پس باید همان یکای انرژی (ژول) را داشته‌ باشد. یکای دیگر گرما، کالری است که در موارد خاصی مورد استفاده قرار می‌گیرد (1cal=4/1860J).

دو جسم کی به تعادل گرمایی می‌رسند؟

دو جسم سرد و گرم را درنظر بگیرید که در تماس با یکدیگر قرار می‌گیرند. بیایید قضیه را از دیدگاه میکروسکوپی بررسی کنیم. در جسم گرم انرژی‌های پتانسیل و جنبشی مربوط به حرکت‌های کاتوره‌ای اتم‌ها، مولکول‌ها و سایر اجزا کاهش می‌یابد. این انرژی‌ها به همین منوال، در داخل جسم سرد افزایش پیدا می‌کنند. این اتفاق آنقدر ادامه پیدا می‌کند تا سرانجام دو جسم، به تعادل گرمایی می‌رسند.

پرسش 4-2

الف) منظور از این جمله که «دماسنج‌ها دمای خودشان را اندازه‌گیری می‌کنند» چیست؟

پاسخ: در واقع دماسنج‌ها، دمای تعادل خود با محیط را اندازه می‌گیرند. پس، دماسنج دمای خود را که در تعادل با محیط است اندازه می‌گیرد.

ب) در یک کلاس درس میز، صندلی، دانش آموز، تخته، شیشه پنجره و … وجود دارد. در یک روز زمستانی، دمای کدام‌یک از آنها بیشتر از دمای هوای اتاق است؟ دمای کدام‌یک کمتر از دمای هوای اتاق است؟

پاسخ: دمای بدن دانش آموز بیشتر از دمای بقیه اجسام است. دمای شیشه پنجره که در تماس با هوای سرد بیرون است، از دمای بقیه اجسام کمتر است. دمای اجسامی مثل میز، صندلی و تخته با دمای هوای اتاق تقریبا یکسان است. ممکن است در تماس دست خود با آنها، دماهای متفاوتی را احساس کنیم. این موارد به خوب یا بد بودن‌ رسانش گرمایی آن اجسام مربوط می‌شود.

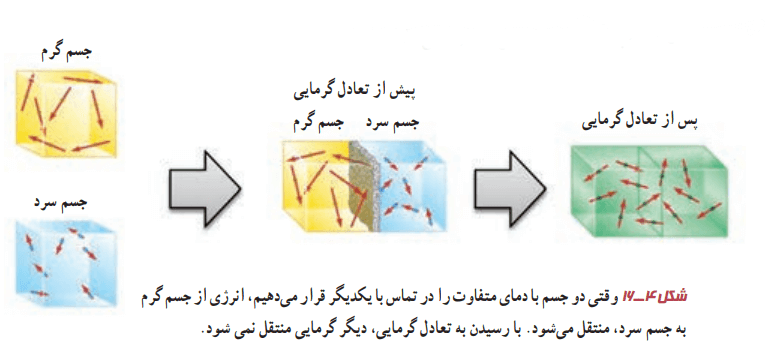
پ) در شکل 4-16 میانگین انرژی جنبشی ذرات دو جسم چگونه تغییر کرده‌ است؟

پاسخ: با کاهش دمای جسم گرم، میانگین انرژی جنبشی ذرات آن کاهش می‌یابد. با افزایش دمای جسم سرد، میانگین انرژی جنبشی ذرات آن افزایش می‌یابد. فرض کنید که دو جسم از یک جنس باشند. در این صورت هنگام برقراری تعادل گرمایی و هم‌دما‌شدن‌ دو جسم، میانگین انرژی جنبشی ذرات آنها با هم مساوی است.

ظرفیت گرمایی

یک پارچ آب سرد را از داخل یخچال بیرون بیاورید و در اتاق قرار دهید. آب از محیط خود، گرما می‌گیرد تا دمایش با دمای اتاق یکی شود. آزمایش نشان می‌دهد که گرمای گرفته‌شده‌ توسط آب با تغییر دمای آب، متناسب است. هرچه آب سردتر باشد، مقدار گرمایی که می‌گیرد تا دمایش با دمای اتاق یکی شود، بیشتر است. فرض می‌کنیم جسمی با محیط اطراف خود، گرمای Q را مبادله می‌کند. در اثر این مبادله گرما، دمای جسم به اندازه ΔT تغییر می‌کند. Q متناسب با ΔT است که ضریب این تناسب را با C نشان می‌دهند، به طوری که:

Q = C ΔT (6-4)

به C، ظرفیت گرمایی جسم گفته‌ می‌شود که به جنس جسم و جرم آن بستگی دارد. در رابطه 4-6 یکای Q، ژول (J) و یکای ΔT، کلوین (K) است. بنابراین، یکای C، ژول بر کلوین (J/K) می‌شود. حالتی را درنظر بگیرید که می‌گوییم ظرفیت گرمایی یک جسم 2000J/K است. در این حالت اگر به آن جسم 2000 ژول گرما بدهیم، دمای آن 1K افزایش پیدا می‌کند. منظور از ظرفیت این نیست که جسم، توانایی محدودی در مبادله گرما دارد. می‌توان گفت تا وقتی که اختلاف دما باشد، مبادله گرما ادامه می‌یابد. مقادیر زیاد آب، مانند آب دریاچه‌ها و دریاها، نوسان‌های دمای هوای اطراف خود را متعادل می‌کند. اگر مقدار آب زیاد باشد، می‌تواند گرمای زیادی را از محیط بگیرد یا به محیط پس بدهد. این شرایط می‌تواند در صورتی اتفاق بیفتد که دمای خود آب، تغییر محسوسی نداشته‌ باشد.

در عکس بالا، تصویری از سواحل قشم را می‌بینید. آب دریا به دلیل داشتن‌ ظرفیت گرمایی زیاد، دمای هوا را متعادل نگه می‌دارد، اما دمای خودش تغییر محسوسی نمی‌کند.

گرمای ویژه

ظرفیت گرمایی اجسامی که از یک نوع ماده ساخته‌ شده‌اند، متناسب با جرم آنهاست. متناسب‌تر آن است که ظرفیت گرمایی واحد جرم اجسام را تعریف کنیم. به آن ظرفیت گرمایی ویژه یا به سادگی گرمای ویژه می‌گویند. گرمای ویژه هر جسم را می‌توان به صورت جمله بعدی تعریف کرد. مقدار گرمایی است که باید به یک کیلوگرم از آن جسم داده‌ شود تا دمای آن، یک درجه سلسیوس ( یا یک کلوین) افزایش یابد. گرمای ویژه را با c نشان می‌دهند. طبق تعریف، رابطه‌اش با ظرفیت گرمایی به‌صورت c=C/m است. در نتیجه رابطه 4-6 چنین می‌شود:

Q = mcΔT (7-4)

در رابطه 4-7 یکای Q، ژول (J) و یکای m، کیلوگرم (kg) و یکای ΔT، کلوین (K) است. بنابراین، یکای c در SI، ژول بر کیلوگرم – کلوین (J/kg.K) است.

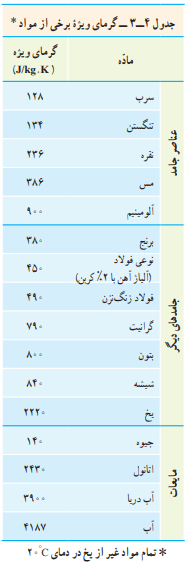
گرمای ویژه یک جسم به جنس ماده تشکیل‌دهنده آن و دما بستگی دارد. گرمای ویژه برخی از مواد در جدول 4-3 داده‌ شده‌ است.

مثال 4-6

مقدار 2 لیتر آب با دمای 20 درجه سانتی‌گراد در اختیار داریم. چقدر گرما لازم است تا دمای این آب را به نقطه جوش آن ( در دمای 100 درجه سانتی‌گراد) برسانیم؟

پاسخ: بر اساس چگالی آب، جرم 1 لیتر آب برابر 1 کیلوگرم است. از جدول 4-3 گرمای ویژه آب 4187 است. بنابراین، گرمای لازم برای گرم کردن‌ 2 کیلوگرم آب، از 20 درجه سانتی‌گراد تا نقطه جوش آن، برابر است با:

Q = m_آبc_آبΔT = (2/0kg) (4187J/kg.°C) (100°C – 20°C) = 6/7 × 10⁵J

استفاده از آب در دستگاه‌های گرم کننده‌ و خنک کننده‌

در جدول 4-3 دیدیم که گرمای ویژه آب از سایر مواد بیشتر است. فرض می‌کنیم یک کیلوگرم آب به اندازه یک درجه سلسیوس تغییر دما می‌دهد. آب در مقایسه با سایر مواد در این حالت، گرمای بیشتری با محیط اطراف خود مبادله می‌کند. از این خاصیت آب برای گرم کردن‌ فضای خانه‌ها به وسیله شوفاژ استفاده می‌شود. آبِ گرم شده‌ در مخزن به وسیله پمپ (تلمبه) و از طریق لوله به رادیاتور می‌رسد. آب در رادیاتور با هوای سرد در تماس است. در نتیجه سرد می‌شود و بخشی از انرژی درونی خود را از دست می‌دهد. بار دیگر، از طریق لوله‌های برگشت، به مخزن برمی‌گردد و در هر چرخه باز همین عمل تکرار می‌شود. از آب برای خنک کردن‌ موتور خودروها نیز استفاده می‌شود.

در محفظه سیلندر و سرسیلندر، مسیرهای عبور آب درنظر گرفته‌ شده‌ است. آب به وسیله تلمبه آب (واترپمپ)، به سرعت در درون این مسیرها گردش می‌کند. در نتیجه این گردش، گرما را از موتور به رادیاتور خودرو می‌برد. هوا از میان پره‌های رادیاتور عبور می‌کند. در اثر این امر، هوا با آب درون رادیاتور تبادل گرمایی می‌کند و آب، انرژی خود را از دست می‌دهد. این آب دوباره به موتور برمی‌گردد و این عمل تکرار می‌شود.

پرسش 4-3

چند گوی فلزی از جنس‌های مختلف، مثلا از آلومینیم، فولاد، برنج، مس، سرب و … را تهیه کنید. باید تمام این گوی‌ها جرم یکسانی داشته‌ باشند. گوی‌ها را توسط ریسمان‌هایی داخل ظرف آبی قرار می‌دهیم که آب آن در حال جوشیدن‌ است. پس از مدتی گوی‌ها را بیرون آورده‌ و آنها را روی یک ورقه پارافین قرار می‌دهیم. به نظر شما کدام گوی، پارافین بیشتری را ذوب می‌کند و علت آن چیست؟ این آزمایش را نخستین بار فیزیک‌دان ایرلندی، جان تیندال طراحی و اجرا کرد.

پاسخ: دمای هر سه‌ گوی یکسان است زیرا هر سه‌، از آب در حال جوشیدن‌ بیرون آمده‌اند. با این حال باید آنها را طبق رابطه Q=mcΔT تک به تک بررسی کنیم. در این میان، گویی که گرمای ویژه بیشتری داشته‌ باشد، پارافین بیشتری را می‌تواند ذوب کند. دلیلش این است که این گوی در فرایند به تعادل رسیدن‌ با دمای محیط، می‌تواند گرمای بیشتری را به محیط بدهد.

جدول 4-3 کتاب را که گرمای ویژه اجسام گوناگون را برحسب J/kg.k آورده‌ است، مشاهده کنید. گرمای ویژه سرب، برنج، مس، فولاد و آلومینیم به ترتیب 128، 380، 386، 450 و 900 است. با این حساب میزان ذوب شدن‌ پارافین از کمترین تا بیشترین نیز به همین ترتیب است.

دمای تعادل

دو یا چند جسم با دماهای مختلف را درنظر بگیرید که در تماس با یکدیگر قرار دارند. آنها پس از مدتی هم‌دما می‌شوند، یعنی دمای آنها به مقدار یکسانی می‌رسد. به این دما، دمای تعادل می‌گویند که می‌توان با استفاده از قانون پایستگی انرژی، آن را محاسبه کرد. در این حالت بعضی از اجسام گرما از دست می‌دهند و بقیه اجسام گرما می‌گیرند. بنا به قرارداد علامت Q برای اجسامی که گرما می‌گیرند مثبت است (0<Q). این علامت برای اجسامی که گرما می‌دهند، منفی اختیار می‌شود (0>Q). با مطالعه رابطه 4-7 می‌توان مواردی را دریافت. با افزایش دما، مقدار مثبتی برای Q به دست می‌آید و با کاهش دما، مقداری منفی برای Q به دست می‌آید. بنا به قانون پایستگی انرژی، همان‌قدر که اجسام گرم انرژی از دست می‌دهند، اجسام سرد انرژی می‌گیرند. با این حساب، جمع جبری این Qها صفر می‌شود:

Q₁ + Q₂ + Q₃ + … = 0 (8-4)

چند جسم متفاوت با گرماهای ویژه c₃، c₂، c₁ و … به جرم‌های m₃، m₂، m₁ و … داریم. آنها را با دماهای اولیه Θ₃، Θ₂، Θ₁ و … در تماس با یکدیگر قرار می‌دهیم. با استفاده از رابطه 4-8 معادله‌ای به دست می‌آوریم که می‌توان دمای تعادل Θ را از آن محاسبه کرد.

m₁c₁ (Θ-Θ₁) + m₂c₂ (Θ-Θ₂) + m₃c₃ (Θ-Θ₃) + … = 0 (9-4)

از معادله 4-9 می‌توانیم برای یافتن‌ کمیت‌های دیگری مانند گرمای ویژه یک جسم نیز استفاده کنیم.

مثال 4-7

شخصی 0.30kg آب 70 درجه سانتی‌گراد را در یک لیوان آلومینیمی 0.12 کیلوگرمی که دمای آن 20 درجه سانتی‌گراد است می‌ریزد. دمای نهایی پس از آنکه آب و لیوان به تعادل گرمایی برسند چقدر است؟ فرض کنید هیچ گرمایی با محیط مبادله نمی‌شود.

پاسخ: با توجه به اینکه هیچ مبادله گرمایی با محیط نداریم، با استفاده از رابطه 4-8 داریم:

0 = Q_آب + Q_{آلومینیم}

اکنون با استفاده از رابطه 4-7 خواهیم داشت:

m_آبc_آب (Θ – Θ_1آب) + m_{آلومینیم}c_{آلومینیم} (Θ – Θ_{1آلومینیم}) = 0

که در آن Θ دمای تعادل مجموعه است. با استفاده از گرماهای ویژه آب و آلومینیم از جدول 4-3 خواهیم داشت:

(0/300kg) (4187J/kg.°C) (Θ – 70°C) + (0/12kg) (9/0 × 10²J/kg.°C) (Θ – 70°C) = 0

و از آنجا پس از اندکی محاسبه جبری برای دمای تعادل، به 66=Θ درجه سانتی‌گراد می‌رسیم.

مثال 4-8

ظرف عایقی حاوی 0/500kg آب با دمای 20 درجه سانتی‌گراد را درنظر بگیرید. در آن یک قطعه مس 0/100 کیلوگرمی با دمای 50 درجه سانتی‌گراد می‌اندازیم. علاوه بر آن یک قطعه فلز دیگر به جرم 0/150kg و به دمای 60 درجه سانتی‌گراد و گرمای ویژه نامعلوم می‌اندازیم. سپس دمای تعادل را اندازه می‌گیریم. دمای تعادل 22 درجه سانتی‌گراد شده‌ است. با چشم‌پوشی از تبادل گرما بین ظرف و سایر اجسام، گرمای ویژه فلز را حساب کنید.

پاسخ: دمای تعادل 22 درجه سانتی‌گراد است و با استفاده از سایر داده‌های این مثال و جدول 4-3 داریم:

آب: m₁ = 0/500kg ، Θ₁ = 20°C ، c₁ = 4187J/kg.°C

مس: m₂ = 0/100kg ، Θ₂ = 50°C ، c₂ = 386J/kg.°C

فلز: m₃ = 0/150kg ، Θ₃ = 60°C ، c₃ = ?

اکنون با استفاده از رابطه 4-9 خواهیم داشت:

m₁c₁ (Θ-Θ₁) + m₂c₂ (Θ-Θ₂) + m₃c₃ (Θ-Θ₃) = 0

(0/500kg) (4187J/kg.°C) (22°C – 20°C) + (0/100kg) (386J/kg.°C) (22°C – 50°C) + (0/150kg) c₃ (22°C – 60°C) = 0

با کمی محاسبه ساده، می‌توان گرمای ویژه فلز را به دست آورد:

c₃ = 545J/kg.°C

تمرین 4-5

جسمی به جرم 0/250kg و دمای 3 درجه سانتی‌گراد را درنظر بگیرید. آن را درون ظرف عایقی حاوی 0/500kg آب با دمای 25 درجه سانتی‌گراد می‌اندازیم. پس از چنددقیقه دمای تعادل را اندازه می‌گیریم. دمای تعادل 21 درجه سانتی‌گراد می‌شود. گرمای ویژه جسم را محاسبه کنید. از تبادل گرما بین ظرف و سایر اجسام چشم‌پوشی کنید.

این تمرین را می‌شود از 2 روش حل کرد.

پاسخ به روش اول:

جسم: m₁ = 0/250kg ، Θ₁ = 3°C ، c₁ = ?

آب: m₂ = 0/500kg ، Θ₂ = 25°C ، c₂ = 4200J/kg.°C

Θ_e = 21°C

پاسخ به روش دوم: در این فرایند آب، گرما از دست می‌دهد و جسم گرما می‌گیرد. در نهایت هر دو به دمای تعادل 21 درجه سانتی‌گراد می‌رسند. به ازای

آب: m₁ = 0/500kg ، Θ₁ = 25°C ، c₁ = 4187J/kg.°C

جسم: m₂ = 0/250kg ، Θ₂ = 3°C

از رابطه 4-10 خواهیم داشت:

به نظرتان چرا جواب دو روش اول و دوم، منفاوت شده‌ است؟ در روش اول گرمای ویژه آب را تقریبی 4200 مبنا قرار دادیم. با این حال در روش دوم، این عدد را به صورت مقدار دقیق آن یعنی 4187 قرار دادیم.

گرماسنج و گرماسنجی

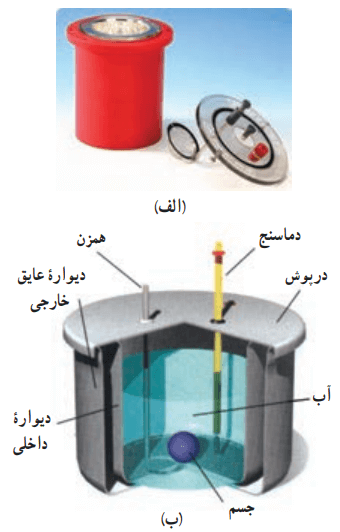
گرماسنج که به آن کالری‌متر نیز می‌گویند شامل ظرفی است درپوش‌دار که به خوبی عایق‌بندی گرمایی شده‌ است. در دو تصویر پایین، عکس واقعی و طرحی از نمای داخلی یک گرماسنج را می‌بینید.

این ظرف در آزمایش‌های گرماسنجی مانند تعیین گرمای ویژه اجسام، به کار می‌رود. در گرماسنج مقداری آب با جرم معین می‌ریزیم. پس از هم‌دما شدن‌ آب و گرماسنج، دمای آب را اندازه می‌گیریم. سپس جسمی را که می‌خواهیم گرمای ویژه‌اش را پیدا کنیم، درون گرماسنج قرار می‌دهیم. این جسم باید جرم و دمای اولیه‌اش مشخص باشد. آنگاه به کمک همزن آب را به هم می‌زنیم تا مجموعه سریع‌تر به دمای تعادل برسد. پس از برقراری تعادل گرمایی، دمای تعادل را اندازه می‌گیریم.

با استفاده از رابطه‌های 4-8 و 4-9 و با چشم‌پوشی از اثر ناچیز دماسنج و همزن در مبادله گرما داریم:

0 = Q_ظرف + Q_جسم + Q_آب

m_آبc_آب (Θ – Θ_1آب) + m_جسمc_جسم (Θ – Θ_1جسم) + m_ظرفc_ظرف (Θ – Θ_1ظرف) = 0

به کمک این رابطه می‌توانیم گرمای ویژه جسم را به دست آوریم. در گرماسنج معمولا جرم و گرمای ویژه ظرف گرماسنج را جداگانه معلوم نمی‌کنند. به جای آن، ظرفیت گرمایی ظرف گرماسنج را مشخص می‌کنند.

مثال 4-9

می‌خواهیم گرمای ویژه فلزی با جنس نامعلوم را اندازه‌گیری کنیم. قطعه‌ای 0/600 کیلوگرمی از آن را تا 100 درجه سانتی‌گراد گرم می‌کنیم. سپس آن را در گرماسنجی با ظرفیت گرمایی 10²×1/80 ژول بر کلوین قرار می‌دهیم. این گرماسنج حاوی 0/500 کیلوگرم آب با دمای اولیه 17/3 درجه سانتی‌گراد است. اگر دمای نهایی مجموعه 20 درجه سانتی‌گراد شود، گرمای ویژه این فلز چقدر است؟

پاسخ: با استفاده از رابطه 4-9 و تعیین ظرفیت گرمایی داریم:

0 = Q_{گرماسنج} + Q_فلز + Q_آب

m_آبc_آب (Θ – Θ_1آب) + m_فلزc_فلز (Θ – Θ_1فلز) + m_{گرماسنج}c_{گرماسنج} (Θ – Θ_{1گرماسنج}) = 0

اکنون با جای گذاری مقادیر خواهیم داشت:

(0/500kg) (4187J/kg.°C) (20°C – 17/3°C) + (0/600kg) c_فلز (20°C – 100°C) + (1/80 × 10²J/°C) (20°C – 17/3°C) = 0

پس از عملیات جبری، گرمای ویژه فلز 128J/kg.°C به دست می‌آید. حالا جدول 4-3 را نگاه می‌کنیم. می‌بینیم که این گرمای ویژه سرب است و احتمالا جنس ماده نامعلوم سرب بوده‌ است.

گرماسنج بمبی

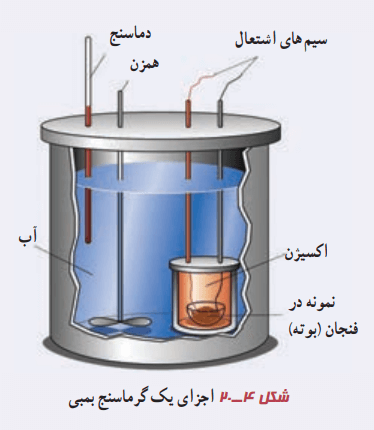
گرماسنج بمبی نوعی گرماسنج است که از آن برای تعیین ارزش غذایی مواد استفاده می‌شود. این امر با اندازه‌گیری انرژی آزاد شده‌ آنها در حین سوختن‌ انجام می‌گیرد. جرم نمونه برای انجام آزمایش باید به دقت اندازه‌گیری شود. به این نمونه که در ظرف سربسته‌ای محتوی اکسیژن قرار می‌گیرد در اصطلاح، بمب می‌گوییم.

سپس این محفظه را در آب یک گرماسنج قرار می‌دهیم. توسط جریان الکتریکی عبوری از یک سیم نازک، نمونه داخل آن سوزانده‌ می‌شود. با اندازه‌گیری تغییر دمای آب، انرژی حاصل از احتراق ماده مورد نظر به دست می‌آید. این مقدار تقریبا معادل انرژی آزاد شده‌ از آن ماده است.